방정식

방정식과 함수의 차이

• 방정식은 함수를 포함한다
  • 모든 함수는 방정식이 될 수 있다
  • 모든 방정식이 함수가 될 수 있는것은 아니다
• 방정식은 미지수의 값에 따라 참이 될 수도 있고 거짓이 될 수도 있다. 변수값들을 내 마음대로 지정할 수 있다
• 함수는 독립변수의 값이 지정되면 반드시 그것에 걸맞는 종속변수 값 딱 하나가 나와야 한다
  • 함수의 종류
    • 일대일 함수
      • 정의역의 서로 다른 원소에 대한 함수값이 다르다
      • 함수값이 같으면 역으로 정의역의 원소도 같다
    • 일대일 대응
      • 위 일대일 함수에서 공역과 치역이 같다는 조건 이 추가되면 됌

      
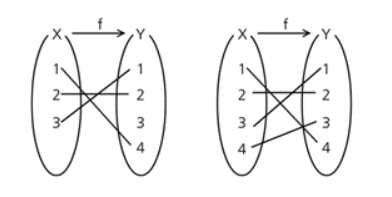
      좌: 일대일 함수, 우: 일대일 대응

• 방정식과 함수의 차이 예시
  • $y = x + 1$
    • 위 식은 $f(x) = x + 1$ 혹은 $y = f(x)$로 표현 가능 (양함수 형태)
    • x = 3이면 y = 4가 되고, x = -3이면 y = -2가 됌
    • 독립변수의 값만 내 맘대로 지정할 수 있으면 함수
  • $y - x - 1 = 0$
    • 위 식은 $f(x, y) = y - x - 1 = 0$로 표현 가능 (음함수 형태)
      • 음함수: 독립변수, 종속변수가 분리되지 않고 하나의 관계식으로 주어지는 함수
    • x = 3, y = 1이면 거짓인 방정식, x = -3, y = -2이면 참인 방정식이 됌
    • 모든 변수의 값을 내 맘대로 지정할 수 있으면 방정식

방정식: 미지수를 포함한 등식 함수: 독립변수와 종속변수의 관계식

방정식, 함수, 도형의 방정식등의 개념 확립