DFS의 경우 함수 초기 부분에 인자로 넘어온 node를 방문처리 해야하며
BFS의 경우 Queue에 삽입하자마자 방문처리 해야한다는 것을 명심 (DFS처럼 반복문 초기 부분에 popleft() 이후 방문처리하면 Queue에 삽입되어있지만 아직 Pop 되지 않은 node들이 중복해서 Queue에 들어오는 경우가 생김)
DFS
개념
가장 깊숙이 위치하는 노드에 닿을 때까지 탐색한다. 다른 말로 최대한 멀리 있는 노드를 우선으로 탐색하는 방식이라고도 한다.

구현을 위한 기능 명시
아래 구현 코드를 보면 stack을 사용하는 것이 명식적으로 보이지 않지만(리스트를 사용하는 것이 보이지 않지만)1, 재귀적 함수 호출 자체가 스택을 활용하는 것으로 생각할 수 있기에 DFS는 스택을 활용한다고 볼 수 있다.
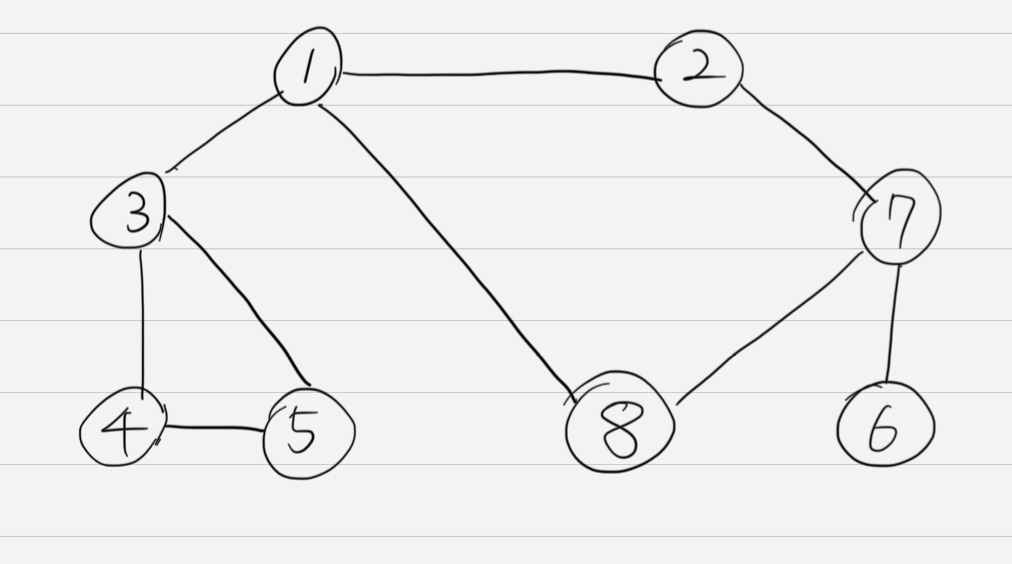
아래 코드 예시에 활용되는 그래프 그림
코드
# DFS 메서드 정의
def dfs(graph, v, visited):
# 현재 노드를 방문 처리
visited[v] = True
print(v, end=' ')
# 현재 노드와 연결된 다른 노드 재귀적 방문
# graph의 각 리스트에 접근하는 인덱스가 곧 노드 번호여서 인덱스 = 노드 번호로 바로 맵핑 가능
# 코딩 테스트에선 대부분 낮은 값의 노드를 우선 방문하는 것으로 되어있음
for i in graph[v]:
if not visited[i]:
dfs(graph, i, visited)
visited = [False] * 9
# 값이 낮은 노드가 먼저 for문에서 선택되기 위해 값 순서대로 정렬화된 모습 확인
# 빈 리스트가 있는 이유는, DFS 함수를 설계할 때 1번 노드부터 최초 실행되는 것으로 설계하였기에
# graph도 인덱스 1부터 의미있는 정보를 담게하기 위해 빈 리스트가 필요하다.
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7],
]
dfs(graph, 1, visited)
1 2 7 6 8 3 4 5
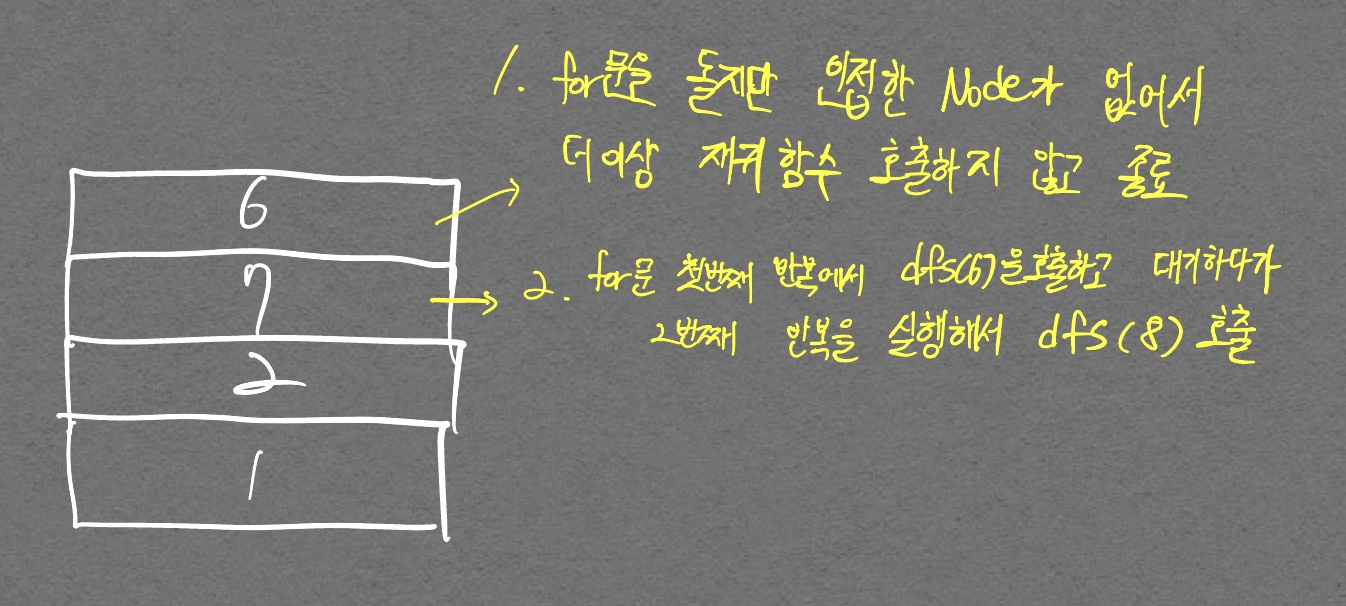
코드 이해를 돕기 위한 그림 (1)
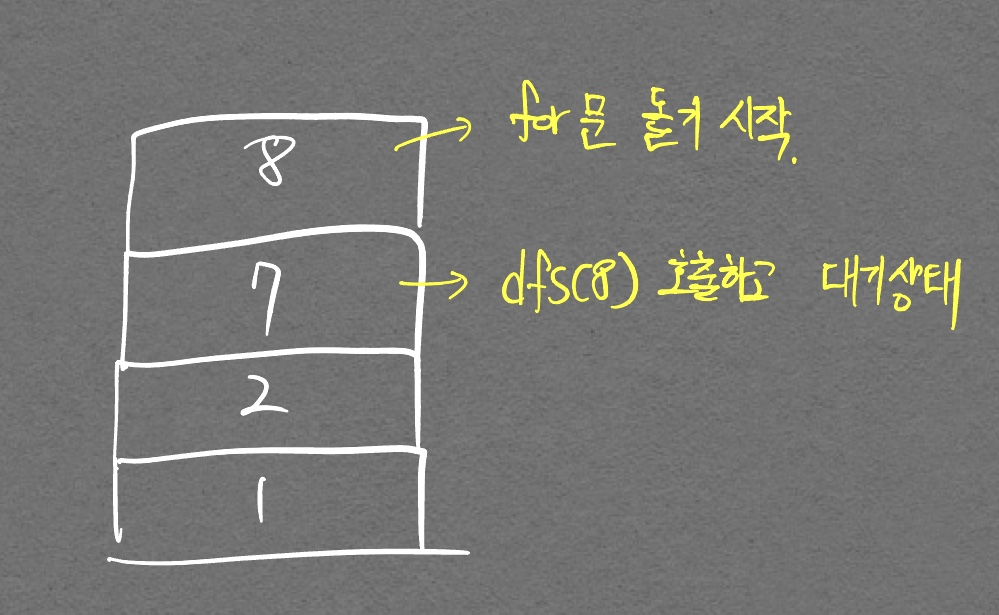
코드 이해를 돕기 위한 그림 (2)
BFS
개념
너비 우선 탐색을 말하며, 가까운 노드부터 탐색하는 알고리즘이다.
- 구현을 위한 기능 명시

DFS와 달리 Queue 자료구조를 사용한다는 점에 주목하자.
Queue는 선입선출 구조이며, 현재 노드에서의 인접한 점을 모두 방문하기 위해 인접한 노드들을 한번에 Queue에 넣는다. (DFS는 하나씩 스택에 넣음)
코드
from collections import deque
# BFS 정의
def bfs(graph, start, visited):
# Queue 구현을 위한 deque 라이브러리 사용
queue = deque([start]) # 맨 처음 함수를 호출할 때 queue에 노드를 삽입하는 것
# 현재 노드를 방문 처리
visited[start] = True
# 큐가 빌 때까지 반복
# 이렇게 while에 바로 엮을 수 있다는것에 주목
# 이런식으로 안하고 break 문 등으로 해결하려고 하면 index error 나면서 출력결과가 안맞아서 오답 될 테니
# 꼭 염두할 것!
while queue:
# 큐에서 하나의 원소를 뽑아 출력
v = queue.popleft()
print(v, end=' ')
# 해당 원소와 연결된, 아직 방문하지 않은 원소들을 큐에 삽입
for i in graph[v]:
if not visited[i]:
queue.append(i)
visited[i] = True
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7],
]
visited = [False] * 9
bfs(graph, 1, visited)
1 2 3 8 7 4 5 6
| DFS | BFS | |
|---|---|---|
| 동작원리 | 스택 | 큐 |
| 구현방법 | 재귀 함수 | 큐 자료구조 이용 |
DFS가 스택 자료구조를 사용한다고 말하지 않는 이유는 단지 재귀함수를 통해 스택 같은 효과를 낸 것이기 때문이다.
반면 BFS는 실제로 Queue 자료구조를 사용하여 구현한다.
문제
p.149 음료수 얼려 먹기
- 해답 코드
n, m = map(int, input().split())
graph = []
for _ in range(n):
graph.append(list(map(int, input())))
def dfs(y, x):
# 주어진 범위를 벗어나는 경우 즉시 종료
# 이건 재귀함수의 종료 조건이라기 보다는 예외처리
if y <= -1 or y >= n or x<= -1 or x >= m:
return False
# 현재 노드를 아직 방문 안했다면
if graph[y][x] == 0:
# 해당 노드 방문 처리
graph[y][x] = 1
#상, 하, 좌, 우 위치에 대해 모두 재귀적으로 호출
dfs(y-1, x)
dfs(y+1, x)
dfs(y, x+1)
dfs(y, x-1)
return True
return False
count = 0
for row in range(n):
for col in range(m):
if dfs(row, col) == True:
count += 1
print(count)
잘못 생각했던 부분이 2가지 있었다.
- BFS로만 풀 수 있다고 생각했다. (인접한 부분 방문만 생각이 들었기 때문)
- DFS로 풀 수 있는 문제이며 이게 왜 DFS인지 의문이 들어 조금 고민해보았다.
- 해답을 보고 DFS로만 풀 수 있는것이겠구나 생각을 했지만, BFS로도 풀 수 있을 것 같아 직접 구현해보았다. (아래 코드 참고)

- 인접 리스트 방식으로 graph를 변경해야 한다고 생각했다.
- 위 코드 구현을 보면 그런 부수작업이 필요 없다는 것을 알 수 있다.
- BFS로 내가 직접 풀은 코드 (보람차다..!)
n, m = map(int, input().split())
graph = []
from collections import deque
for _ in range(n):
graph.append(list(map(int, input())))
def bfs(y, x):
# if y <= -1 or y >= n or x <= -1 or x >= m:
# return False
queue = deque([(y, x)])
# 방문 처리
graph[y][x] = 1
while queue:
coor = queue.popleft()
dy, dx = coor[0], coor[1]
if dy-1 >= 0 and graph[dy-1][dx] == 0:
queue.append((dy-1, dx))
graph[dy-1][dx] = 1
if dy+1 < n and graph[dy+1][dx] == 0:
queue.append((dy+1, dx))
graph[dy+1][dx] = 1
if dx-1 >= 0 and graph[dy][dx-1] == 0:
queue.append((dy, dx-1))
graph[dy][dx-1] = 1
if dx+1 < m and graph[dy][dx+1] == 0:
queue.append((dy, dx+1))
graph[dy][dx+1] = 1
return True
count = 0
for row in range(n):
for col in range(m):
if graph[row][col] == 0:
count += 1
bfs(row, col)
# if (row, col) == True: # 이걸 호출하는게 아니지.. 이러면 그냥 bfs 20번 호출한거니 20이 나오지..
# count += 1
print(count)
15 14
00000111100000
11111101111110
11011101101110
11011101100000
11011111111111
11011111111100
11000000011111
01111111111111
00000000011111
01111111111000
00011111111000
00000001111000
11111111110011
11100011111111
11100011111111
8
- 위 코드 핵심 부분을 최적화하면 아래와 같다
# if dy-1 >= 0 and graph[dy-1][dx] == 0:
# queue.append((dy-1, dx))
# graph[dy-1][dx] = 1
# if dy+1 < n and graph[dy+1][dx] == 0:
# queue.append((dy+1, dx))
# graph[dy+1][dx] = 1
# if dx-1 >= 0 and graph[dy][dx-1] == 0:
# queue.append((dy, dx-1))
# graph[dy][dx-1] = 1
# if dx+1 < m and graph[dy][dx+1] == 0:
# queue.append((dy, dx+1))
# graph[dy][dx+1] = 1
# 위 주석한 부분 대체
if (0 <= ny and ny < n) and (0 <= nx and nx < m) and graph[ny][nx] == 0:
queue.append((ny, nx))
graph[ny][nx] = 1
p.153 미로 탈출
DFS, BFS중 어떤 방법으로 풀어야 할지 감이 오지 않아서 DFS로 풀었다.
구현하는데 있어서 스스로 Edge Case를 만들어가면서 DFS 알고리즘이 내 의도대로 완벽하게 돌아가도록 단계별로 구현하였다.
- 첫번째 구현
import copy
N, M = map(int, input().split())
graph = [list(map(int, input())) for _ in range(N)]
# visit = [[False]*M for _ in range(N)]
cnt = 0
answer = 1e+10
def dfs(x, y):
global cnt
# global answer
# print(f"{x, y}로 이동")
cnt+=1
if x == N-1 and y == M-1:
return True, cnt
# visit[x][y] = True
dir = [(1, 0), (0, 1), (0, -1), (-1, 0)]
for dx, dy in dir:
nx, ny = x+dx, y+dy
# if 0 <= nx < N and 0 <= ny < M and graph[nx][ny] == 1 and not visit[nx][ny]:
if 0 <= nx < N and 0 <= ny < M and graph[nx][ny] == 1:
# reached, result = dfs(nx, ny, cnt, copy.deepcopy(visit))
reached, result = dfs(nx, ny)
if reached: # 끝까지 도달 했으면
# answer = min(answer, result)
# print(f"{answer}로 갱신")
return True, result
return False, 0
# dfs(0, 0)
_, answer = dfs(0, 0)
print(answer)
5 6
101010
111111
000001
111111
111111
10
막연하게 DFS를 구현하다가 방문 처리를 하지 않았는데도 정답이 출력되는 것을 보고 방문 처리 할 필요가 없는 것인가 잠시 고민하면서 Edge Case를 만들어봤다.
다음이 엣지 케이스의 입력이다.
6 5
11111
00001
11101
10111
10000
11111
방문 처리를 하지 않았기 때문에 주황색 좌표에서 호출한 파랑색 좌표 에서 다시 주황색 좌표를 호출하기 때문에 무한루프에 빠진다.
그래서 다음 코드와 같이 방문처리를 진행하니 위의 Edge Case는 통과되었다.
import copy
N, M = map(int, input().split())
graph = [list(map(int, input())) for _ in range(N)]
visit = [[False]*M for _ in range(N)]
cnt = 0
answer = 1e+10
def dfs(x, y):
global cnt
# global answer
# print(f"{x, y}로 이동")
cnt+=1
if x == N-1 and y == M-1:
return True, cnt
visit[x][y] = True
dir = [(1, 0), (0, 1), (0, -1), (-1, 0)]
for dx, dy in dir:
nx, ny = x+dx, y+dy
if 0 <= nx < N and 0 <= ny < M and graph[nx][ny] == 1 and not visit[nx][ny]:
# reached, result = dfs(nx, ny, cnt, copy.deepcopy(visit))
reached, result = dfs(nx, ny)
if reached: # 끝까지 도달 했으면
# answer = min(answer, result)
# print(f"{answer}로 갱신")
return True, result
return False, 0
# dfs(0, 0)
_, answer = dfs(0, 0)
print(answer)
하지만 아래와 같은 Case가 입력된다면 어떨까?
7 5
11111
00001
11101
10111
10100
10000
11111
우린 정답이 21이 나오길 원하지만 22가 나오게 된다. 그 이유는 아래 그림으로 설명하겠다.

모든 재귀함수에서 전역변수 cnt에 접근해서 방문할 때 마다 1씩 올리고 있으므로 22가 출력된다. 어떻게 하면 파란색 좌표로의 cnt를 무시하게 할 수 있을까?
정답은 각 호출된 함수별로 자신만의 cnt값을 가지고 있으면 된다. 그래서 아래와 같이 코드를 짜면 위 문제가 해결되게 된다. 이해가 가지 않는다면 재귀 함수 포스팅을 보고 깊이 생각해 보자.
import copy
N, M = map(int, input().split())
graph = [list(map(int, input())) for _ in range(N)]
visit = [[False]*M for _ in range(N)]
cnt = 0
answer = 1e+10
def dfs(x, y, cnt):
# global answer
# print(f"{x, y}로 이동")
cnt+=1
if x == N-1 and y == M-1:
return True, cnt
visit[x][y] = True
dir = [(1, 0), (0, 1), (0, -1), (-1, 0)]
for dx, dy in dir:
nx, ny = x+dx, y+dy
if 0 <= nx < N and 0 <= ny < M and graph[nx][ny] == 1 and not visit[nx][ny]:
# reached, result = dfs(nx, ny, cnt, copy.deepcopy(visit))
reached, result = dfs(nx, ny, cnt)
if reached: # 끝까지 도달 했으면
# answer = min(answer, result)
# print(f"{answer}로 갱신")
return True, result
return False, 0
# dfs(0, 0)
_, answer = dfs(0, 0, cnt)
print(answer)
마지막으로 생각해낸 Edge Case는 다음과 같다.
7 7
1111111
0000001
1111101
1010111
1011100
1000000
1111111
도착할 수 있는 경로가 2가지가 있으며 각각 27, 29이다. 우린 27이 정답으로 나오길 원하지만 우리가 구현한 DFS 문제에는 다음의 2가지 문제점이 있다.
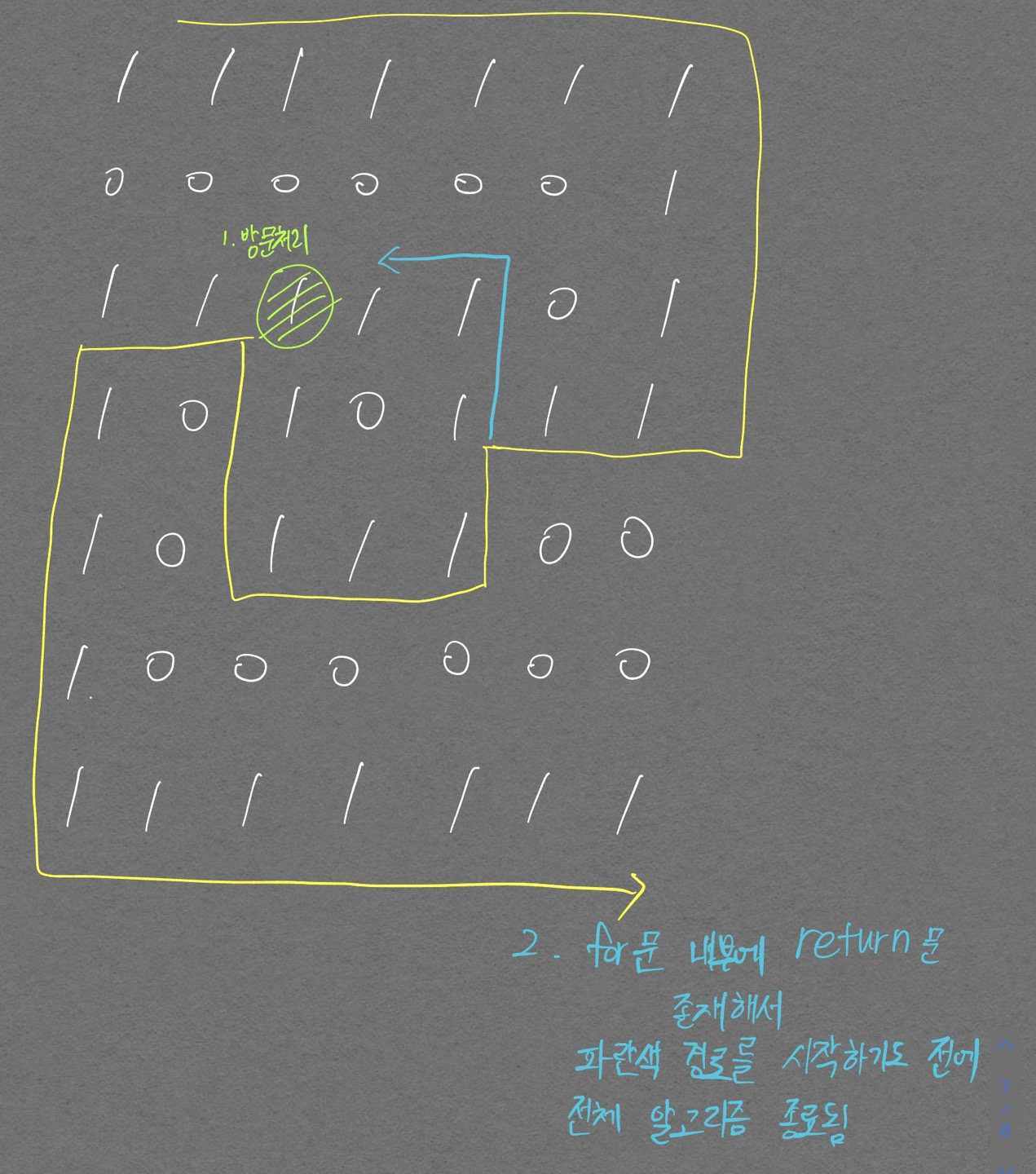
- 노란색 좌표로 이동하면서 그림에 표시하였듯 경로가 겹치는 부분이 방문처리가 되어서 파란색 좌표를 통한 경로가 지나갈 수가 없게됨. 2. 애초에
return 문이for 문내부에 존재하기 때문에 파란색 경로를 시작하기도 전에 전체 알고리즘이 종료되어 버림
따라서 for 문에 있는 return문을 지워버리고 cnt 변수를 각 호출된 함수에서 따로 값을 가지고 있던것처럼 visit 리스트도 각 호출된 함수가 값을 가지고 있게 구현하였다. 리스트는 mutable 객체이기 때문에 copy.deepcopy()로 넘겨줘야 각 함수별로 다른 visit 리스트를 가지게 된다. 코드는 다음과 같다.
import copy
N, M = map(int, input().split())
graph = [list(map(int, input())) for _ in range(N)]
visit = [[False]*M for _ in range(N)]
cnt = 0
answer = 1e+10
def dfs(x, y, cnt, visit):
global answer
cnt+=1
if x == N-1 and y == M-1:
return True, cnt
visit[x][y] = True
dir = [(1, 0), (0, 1), (0, -1), (-1, 0)]
for dx, dy in dir:
nx, ny = x+dx, y+dy
if 0 <= nx < N and 0 <= ny < M and graph[nx][ny] == 1 and not visit[nx][ny]:
reached, result = dfs(nx, ny, cnt, copy.deepcopy(visit))
# reached, result = dfs(nx, ny, cnt)
if reached: # 끝까지 도달 했으면
answer = min(answer, result)
# return True, answer
return False, 1e+10
dfs(0, 0, cnt, visit)
# _, answer = dfs(0, 0, cnt)
print(answer)
하지만 위 코드는 공간복잡도가 굉장히 커지게 되서 상당히 비효율적인 코드가 된다.
정말 많은 여정을 달려왔고, 이제 마지막으로 BFS를 활용한 정답 코드를 보자.
from collections import deque
n, m = map(int, input().split())
graph = []
for i in range(n):
graph.append(list(map(int, input())))
dx = [-1, 1, 0, 0]
dy = [0 ,0, -1, 1]
def bfs(x, y):
queue = deque()
queue.append((x, y))
while queue:
x, y = queue.popleft()
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if nx < 0 or ny < 0 or nx >= n or ny >= m:
continue
if graph[nx][ny] == 0:
continue
if graph[nx][ny] == 1:
graph[nx][ny] = graph[x][y] + 1
queue.append((nx, ny))
return graph[n-1][m-1]
print(bfs(0, 0))
7 7
1111111
0000001
1111101
1010111
1011100
1000000
1111111
27
따로 방문처리를 하기 보다는 graph[nx][ny] == 1 를 통해 이전에 지나갔는지 아닌지를 판단하고 있다.
이 개념을 BFS, DFS에 적용했을 때의 차이는 다음과 같다.
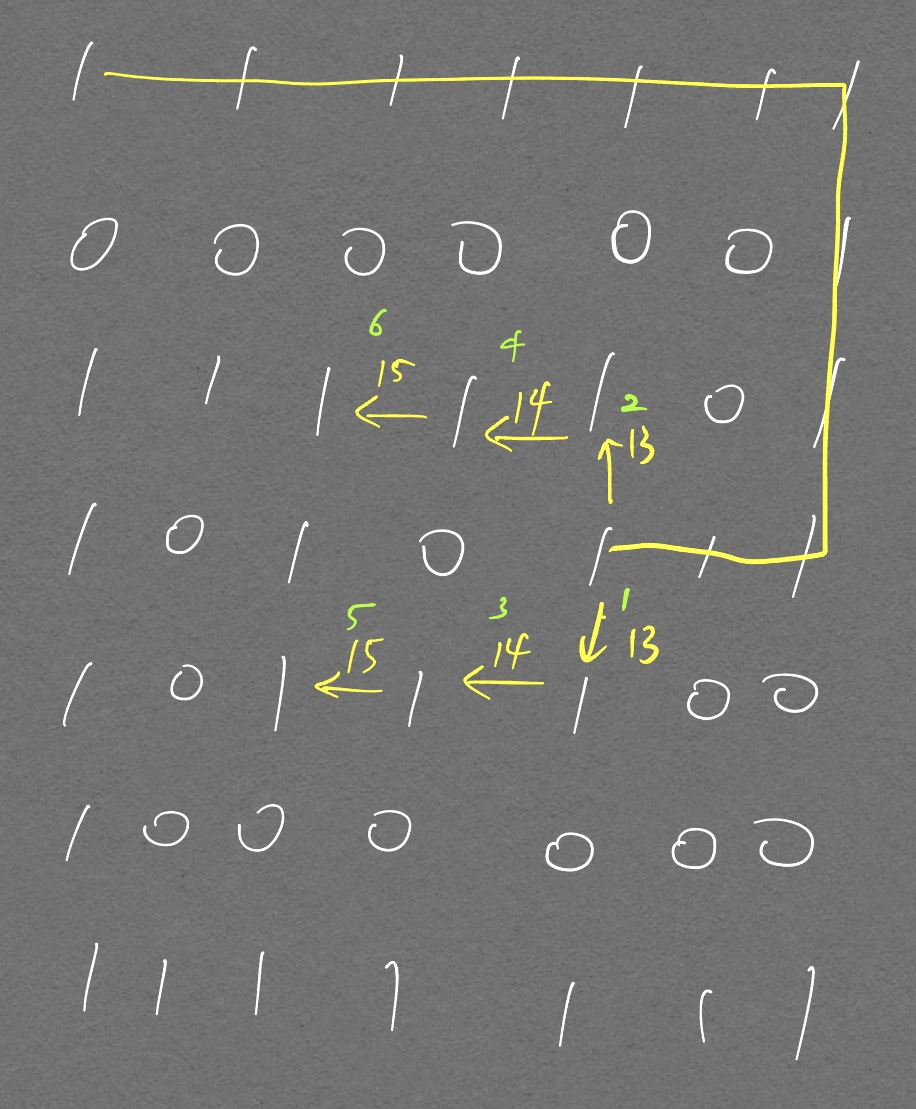
초록색 숫자가 호출 순서이며, 노란색 숫자가 cnt 값이다. 상대적으로 빠른 경로를 먼저 1에서 cnt + 1값으로 대체시키기 때문에 최단거리가 출력될 수 있다.
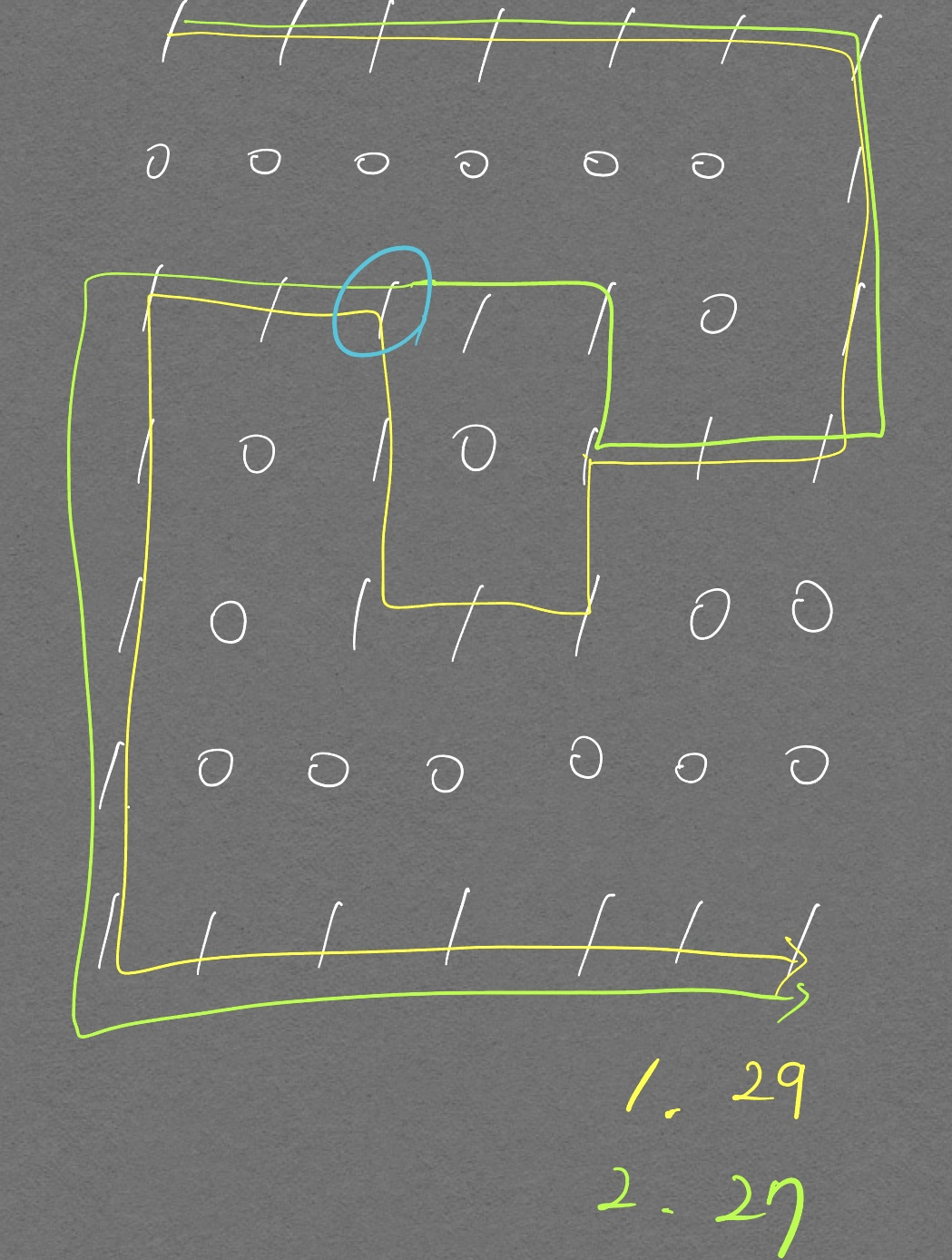
DFS 일 때 2가지 값이 나오기 때문에 BFS에 비해 복잡하게 구현해야 한다.
깨알팁
DFS 문제를 풀다 보면 순열, 조합을 구현해야 하는 경우가 발생한다.
DFS로 순열을 구현할 땐 visit 테이블을 통해 방문 처리를 해줘야 하지만, 조합을 구현할 땐 visit 테이블 필요없이 idx만 잘 조정해주면 된다.
구현 실수 줄이기
BFS
백준: 2178번을 통해 BFS에서 흔히 발생할 수 있는 실수를 기억해두자.
위 문제는 2가지 방식으로 풀 수 있다.
- 여태까지 온 거리를 누적시키면서 방문하는 위치의 matrix값 변경
- queue에 distance 변수를 통해 현재까지 온 경로에 대한 최단 거리를 저장하게 끔 구현
위 2번 방법에서 다음과 같은 실수를 조심하자
import sys
from collections import deque
def solution():
global n, m
answer = 0
n, m = map(int, sys.stdin.readline().rstrip().split())
matrix = []
for _ in range(n):
matrix.append(list(map(int, sys.stdin.readline().rstrip())))
visit = [[False]*m for _ in range(n)]
return bfs(matrix, visit)
def bfs(matrix, visit):
q = deque()
distance = 0
dx = [-1, 0, 1, 0]
dy = [0, 1, 0, -1]
# 방문 처리
distance += 1
q.append([0, 0, distance])
visit[0][0] = True
while q:
cx, cy, c_distance = q.popleft()
if cx == n-1 and cy == m-1:
return c_distance
for i in range(4):
nx, ny = dx[i] + cx, dy[i] + cy
if 0<= nx < n and 0<= ny < m and not visit[nx][ny] and matrix[nx][ny] != 0:
c_distance += 1
q.append([nx, ny, c_distance])
visit[nx][ny] = True
print(solution())
위 코드에서 잘못된 부분을 찾아보자. c_distance 변수를 통해 최단 경로를 BFS 탐색의 매 순간마다 활용하도록 하고 있다. 하지만 위 처럼 구현할 경우 for문을 4번 반복하면서 최악의 경우에는 한칸을 이동하는데, c_disntace는 기존보다 4 증가할수 있다. 위 처럼 구현하지 말고, 반드시 q.append([nx, ny, c_disntace +1]) 형태로 구성해서 for문에 영향받지 않도록 해야한다.
방문처리 하기
BFS, DFS 알고리즘 구현이 어느정도 익숙해지면서 다음과 같은 의문이 들었다.
어떨땐 방문처리 코드 구현 필요가 없고, 어떨때는 필요한 것 같은데 이 구분이 어떻게 되지?
먼저, 5개의 숫자 (0, 1, 2, 3, 4) 중 3개를 뽑는(즉, 순서 상관 없음) 코드를 DFS로 구현해보자.
explorer = []
def dfs(depth, idx):
if depth >= 3:
print(explorer)
return
for i in range(idx, 5):
explorer.append(i)
dfs(depth+1, i+1)
explorer.pop()
dfs(0, 0)
위 코드는 방문 처리를 하지 않는다. 왜 방문처리를 하지 않는게 가능할까? 바로 다음 그림 때문이다.
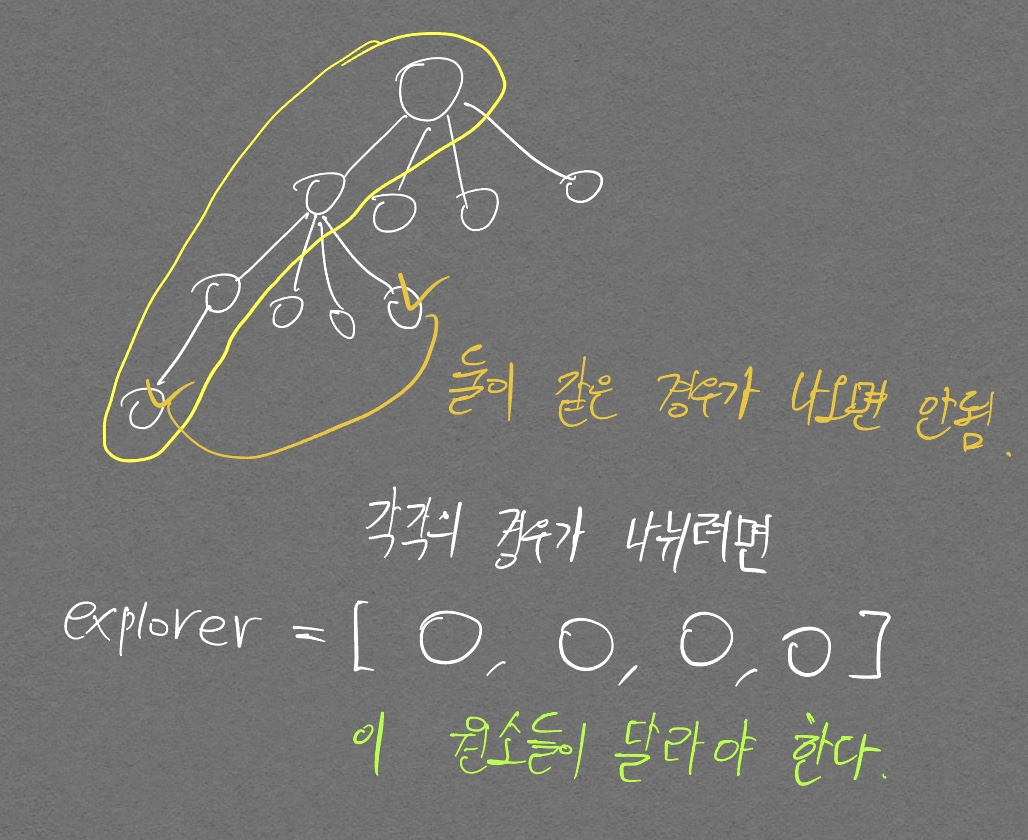
for문의 인덱스를 통해 explorer에 들어가는 값이 정해지는데, 이 인덱스는 dfs 알고리즘의 depth가 깊어질수록 제한되게 된다. 이와 같은 이유로 이미 탐색한 경우(5개 중 3개 뽑은 경우)와 다른 경로로 탐색한 경우가 겹치지 않게 된다.
-
파이썬은 리스트를 통해 스택 자료구조를 구현할 수 있다. ↩