문제
신용카드 사기 검출
데이터 링크
클래스 0: 정상적인 트랜잭션 클래스 1: 사기 트랜잭션
분석
- 사기 검출, 이상 검출등은 레이블 값이 불균형한 경우가 많음. 대부분 정상이고 극소수가 비정상이기 때문
- 이를 해결하기 위한 기법
- Oversampling
- 이상 데이터와 같은 적은 데이터 세트를 증식시켜 충분한 데이터를 확보함
- 동일한 데이터를 증식시키는건 과적합 되기 때문에 의미가 없으므로 원본 데이터 피쳐 값들을 아주 약간만 변형시켜 증식시킴
- 대표적 증식방법으로 SMOTE(Synthetic Minority Over-Sampling Technique) 존재
- SMOTE는 개별 데이터들의 K 최근접 이웃(K Nearest Neighbor)을 찾아서 이 데이터와 K 이웃들의 차이를 일정 값으로 만들어서 기존 데이터와 약간 차이나는 새로운 데이터를 생성하는 방식
- 대표적 증식방법으로 SMOTE(Synthetic Minority Over-Sampling Technique) 존재
- Undersampling
- 많은 레이블을 가진 데이터 세트를 적은 데이터 세트 수준으로 감소시킴
- Oversampling
혼자 간단하게 전처리, 학습 및 성능도출 해보기
import pandas as pd
pd.set_option('display.max_rows', 500)
pd.set_option('display.max_columns', 500)
pd.set_option('display.width', 1000)
import numpy as np
import matplotlib.pyplot as plt
card_df = pd.read_csv('./creditcard.csv')
card_df.head(3)
| Time | V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | V10 | V11 | V12 | V13 | V14 | V15 | V16 | V17 | V18 | V19 | V20 | V21 | V22 | V23 | V24 | V25 | V26 | V27 | V28 | Amount | Class | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | -1.359807 | -0.072781 | 2.536347 | 1.378155 | -0.338321 | 0.462388 | 0.239599 | 0.098698 | 0.363787 | 0.090794 | -0.551600 | -0.617801 | -0.991390 | -0.311169 | 1.468177 | -0.470401 | 0.207971 | 0.025791 | 0.403993 | 0.251412 | -0.018307 | 0.277838 | -0.110474 | 0.066928 | 0.128539 | -0.189115 | 0.133558 | -0.021053 | 149.62 | 0 |
| 1 | 0.0 | 1.191857 | 0.266151 | 0.166480 | 0.448154 | 0.060018 | -0.082361 | -0.078803 | 0.085102 | -0.255425 | -0.166974 | 1.612727 | 1.065235 | 0.489095 | -0.143772 | 0.635558 | 0.463917 | -0.114805 | -0.183361 | -0.145783 | -0.069083 | -0.225775 | -0.638672 | 0.101288 | -0.339846 | 0.167170 | 0.125895 | -0.008983 | 0.014724 | 2.69 | 0 |
| 2 | 1.0 | -1.358354 | -1.340163 | 1.773209 | 0.379780 | -0.503198 | 1.800499 | 0.791461 | 0.247676 | -1.514654 | 0.207643 | 0.624501 | 0.066084 | 0.717293 | -0.165946 | 2.345865 | -2.890083 | 1.109969 | -0.121359 | -2.261857 | 0.524980 | 0.247998 | 0.771679 | 0.909412 | -0.689281 | -0.327642 | -0.139097 | -0.055353 | -0.059752 | 378.66 | 0 |
card_df.info() # Null 값 여부 check
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 284807 entries, 0 to 284806
Data columns (total 31 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Time 284807 non-null float64
1 V1 284807 non-null float64
2 V2 284807 non-null float64
3 V3 284807 non-null float64
4 V4 284807 non-null float64
5 V5 284807 non-null float64
6 V6 284807 non-null float64
7 V7 284807 non-null float64
8 V8 284807 non-null float64
9 V9 284807 non-null float64
10 V10 284807 non-null float64
11 V11 284807 non-null float64
12 V12 284807 non-null float64
13 V13 284807 non-null float64
14 V14 284807 non-null float64
15 V15 284807 non-null float64
16 V16 284807 non-null float64
17 V17 284807 non-null float64
18 V18 284807 non-null float64
19 V19 284807 non-null float64
20 V20 284807 non-null float64
21 V21 284807 non-null float64
22 V22 284807 non-null float64
23 V23 284807 non-null float64
24 V24 284807 non-null float64
25 V25 284807 non-null float64
26 V26 284807 non-null float64
27 V27 284807 non-null float64
28 V28 284807 non-null float64
29 Amount 284807 non-null float64
30 Class 284807 non-null int64
dtypes: float64(30), int64(1)
memory usage: 67.4 MB
card_df.describe()
| Time | V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | V10 | V11 | V12 | V13 | V14 | V15 | V16 | V17 | V18 | V19 | V20 | V21 | V22 | V23 | V24 | V25 | V26 | V27 | V28 | Amount | Class | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 284807.000000 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 284807.000000 | 284807.000000 |
| mean | 94813.859575 | 3.918649e-15 | 5.682686e-16 | -8.761736e-15 | 2.811118e-15 | -1.552103e-15 | 2.040130e-15 | -1.698953e-15 | -1.893285e-16 | -3.147640e-15 | 1.772925e-15 | 9.289524e-16 | -1.803266e-15 | 1.674888e-15 | 1.475621e-15 | 3.501098e-15 | 1.392460e-15 | -7.466538e-16 | 4.258754e-16 | 9.019919e-16 | 5.126845e-16 | 1.473120e-16 | 8.042109e-16 | 5.282512e-16 | 4.456271e-15 | 1.426896e-15 | 1.701640e-15 | -3.662252e-16 | -1.217809e-16 | 88.349619 | 0.001727 |
| std | 47488.145955 | 1.958696e+00 | 1.651309e+00 | 1.516255e+00 | 1.415869e+00 | 1.380247e+00 | 1.332271e+00 | 1.237094e+00 | 1.194353e+00 | 1.098632e+00 | 1.088850e+00 | 1.020713e+00 | 9.992014e-01 | 9.952742e-01 | 9.585956e-01 | 9.153160e-01 | 8.762529e-01 | 8.493371e-01 | 8.381762e-01 | 8.140405e-01 | 7.709250e-01 | 7.345240e-01 | 7.257016e-01 | 6.244603e-01 | 6.056471e-01 | 5.212781e-01 | 4.822270e-01 | 4.036325e-01 | 3.300833e-01 | 250.120109 | 0.041527 |
| min | 0.000000 | -5.640751e+01 | -7.271573e+01 | -4.832559e+01 | -5.683171e+00 | -1.137433e+02 | -2.616051e+01 | -4.355724e+01 | -7.321672e+01 | -1.343407e+01 | -2.458826e+01 | -4.797473e+00 | -1.868371e+01 | -5.791881e+00 | -1.921433e+01 | -4.498945e+00 | -1.412985e+01 | -2.516280e+01 | -9.498746e+00 | -7.213527e+00 | -5.449772e+01 | -3.483038e+01 | -1.093314e+01 | -4.480774e+01 | -2.836627e+00 | -1.029540e+01 | -2.604551e+00 | -2.256568e+01 | -1.543008e+01 | 0.000000 | 0.000000 |
| 25% | 54201.500000 | -9.203734e-01 | -5.985499e-01 | -8.903648e-01 | -8.486401e-01 | -6.915971e-01 | -7.682956e-01 | -5.540759e-01 | -2.086297e-01 | -6.430976e-01 | -5.354257e-01 | -7.624942e-01 | -4.055715e-01 | -6.485393e-01 | -4.255740e-01 | -5.828843e-01 | -4.680368e-01 | -4.837483e-01 | -4.988498e-01 | -4.562989e-01 | -2.117214e-01 | -2.283949e-01 | -5.423504e-01 | -1.618463e-01 | -3.545861e-01 | -3.171451e-01 | -3.269839e-01 | -7.083953e-02 | -5.295979e-02 | 5.600000 | 0.000000 |
| 50% | 84692.000000 | 1.810880e-02 | 6.548556e-02 | 1.798463e-01 | -1.984653e-02 | -5.433583e-02 | -2.741871e-01 | 4.010308e-02 | 2.235804e-02 | -5.142873e-02 | -9.291738e-02 | -3.275735e-02 | 1.400326e-01 | -1.356806e-02 | 5.060132e-02 | 4.807155e-02 | 6.641332e-02 | -6.567575e-02 | -3.636312e-03 | 3.734823e-03 | -6.248109e-02 | -2.945017e-02 | 6.781943e-03 | -1.119293e-02 | 4.097606e-02 | 1.659350e-02 | -5.213911e-02 | 1.342146e-03 | 1.124383e-02 | 22.000000 | 0.000000 |
| 75% | 139320.500000 | 1.315642e+00 | 8.037239e-01 | 1.027196e+00 | 7.433413e-01 | 6.119264e-01 | 3.985649e-01 | 5.704361e-01 | 3.273459e-01 | 5.971390e-01 | 4.539234e-01 | 7.395934e-01 | 6.182380e-01 | 6.625050e-01 | 4.931498e-01 | 6.488208e-01 | 5.232963e-01 | 3.996750e-01 | 5.008067e-01 | 4.589494e-01 | 1.330408e-01 | 1.863772e-01 | 5.285536e-01 | 1.476421e-01 | 4.395266e-01 | 3.507156e-01 | 2.409522e-01 | 9.104512e-02 | 7.827995e-02 | 77.165000 | 0.000000 |
| max | 172792.000000 | 2.454930e+00 | 2.205773e+01 | 9.382558e+00 | 1.687534e+01 | 3.480167e+01 | 7.330163e+01 | 1.205895e+02 | 2.000721e+01 | 1.559499e+01 | 2.374514e+01 | 1.201891e+01 | 7.848392e+00 | 7.126883e+00 | 1.052677e+01 | 8.877742e+00 | 1.731511e+01 | 9.253526e+00 | 5.041069e+00 | 5.591971e+00 | 3.942090e+01 | 2.720284e+01 | 1.050309e+01 | 2.252841e+01 | 4.584549e+00 | 7.519589e+00 | 3.517346e+00 | 3.161220e+01 | 3.384781e+01 | 25691.160000 | 1.000000 |
# Time value는 별로 중요할 것 같지않아서 drop
card_df.drop('Time', axis=1, inplace=True)
card_df.head()
from sklearn.model_selection import train_test_split
feature = card_df.iloc[:, :-1]
label = card_df.iloc[:, -1]
X_train, X_test, y_train, y_test = train_test_split(feature, label)
X_train.shape, X_test.shape, y_train.shape, y_test.shape
((213605, 29), (71202, 29), (213605,), (71202,))
from lightgbm import LGBMClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import roc_auc_score, accuracy_score
clf = LGBMClassifier(n_estimators=100) # 초기 빠른 하이퍼 파라미터 설정을 위해 estimator 갯수 작게
params = {'max_depth': [5, 10, 15]} # 과적합 방지용으로 하이퍼 파라미터 몇개 알고있지만, 적절한 값에 대한 기준을 잘 몰라서 일단 max_depth만 조절해보자
gridCV = GridSearchCV(clf, n_jobs=-1, param_grid=params, cv=3)
evals = [(X_test, y_test)]
gridCV.fit(X_train, y_train, eval_set=evals, early_stopping_rounds=30, eval_metric='auc')
preds = gridCV.predict(X_test)
probs = gridCV.predict_proba(X_test)[:, -1]
accuracy = accuracy_score(y_test, preds)
roc = roc_auc_score(y_test, preds)
print(f'Accuracy score: {accuracy:.4f} roc score: {roc:.4f}')
[1] valid_0's auc: 0.965227 valid_0's binary_logloss: 0.00936288
[2] valid_0's auc: 0.562286 valid_0's binary_logloss: 0.0285558
[3] valid_0's auc: 0.660567 valid_0's binary_logloss: 0.0214766
[4] valid_0's auc: 0.847699 valid_0's binary_logloss: 0.0146109
[5] valid_0's auc: 0.838775 valid_0's binary_logloss: 0.0252176
[6] valid_0's auc: 0.839122 valid_0's binary_logloss: 0.0191823
[7] valid_0's auc: 0.837369 valid_0's binary_logloss: 0.01829
[8] valid_0's auc: 0.828801 valid_0's binary_logloss: 0.0188107
[9] valid_0's auc: 0.829557 valid_0's binary_logloss: 0.0195046
[10] valid_0's auc: 0.811758 valid_0's binary_logloss: 0.0205142
[11] valid_0's auc: 0.811364 valid_0's binary_logloss: 0.022583
[12] valid_0's auc: 0.766871 valid_0's binary_logloss: 0.0228871
[13] valid_0's auc: 0.811503 valid_0's binary_logloss: 0.0215574
[14] valid_0's auc: 0.814388 valid_0's binary_logloss: 0.0246988
[15] valid_0's auc: 0.805495 valid_0's binary_logloss: 0.0282179
[16] valid_0's auc: 0.805208 valid_0's binary_logloss: 0.0286174
[17] valid_0's auc: 0.807372 valid_0's binary_logloss: 0.0279136
[18] valid_0's auc: 0.810976 valid_0's binary_logloss: 0.0243398
[19] valid_0's auc: 0.816831 valid_0's binary_logloss: 0.0241958
[20] valid_0's auc: 0.816681 valid_0's binary_logloss: 0.0246229
[21] valid_0's auc: 0.816423 valid_0's binary_logloss: 0.0241755
[22] valid_0's auc: 0.814858 valid_0's binary_logloss: 0.0260238
[23] valid_0's auc: 0.600747 valid_0's binary_logloss: 0.0363027
[24] valid_0's auc: 0.619092 valid_0's binary_logloss: 0.0352866
[25] valid_0's auc: 0.807625 valid_0's binary_logloss: 0.0330898
[26] valid_0's auc: 0.759556 valid_0's binary_logloss: 0.033595
[27] valid_0's auc: 0.878665 valid_0's binary_logloss: 0.0311388
[28] valid_0's auc: 0.788262 valid_0's binary_logloss: 0.0317903
[29] valid_0's auc: 0.779519 valid_0's binary_logloss: 0.0288819
[30] valid_0's auc: 0.779187 valid_0's binary_logloss: 0.0289138
[31] valid_0's auc: 0.78883 valid_0's binary_logloss: 0.0305115
Accuracy score: 0.9994 roc score: 0.9239
from lightgbm import plot_importance
clf = LGBMClassifier(n_estimators=100, max_depth=5)
clf.fit(X_train, y_train, early_stopping_rounds=30, eval_metric='auc', eval_set=[(X_test, y_test)])
plot_importance(clf)
plt.show()
# plt.plot(clf.feature_importances_)
# fig, ax = plt.subplots(1,1,figsize=(10,8))
# plot_importance(xgb_clf, ax=ax , max_num_features=20,height=0.4)
[1] valid_0's auc: 0.965227 valid_0's binary_logloss: 0.00936288
[2] valid_0's auc: 0.562286 valid_0's binary_logloss: 0.0285558
[3] valid_0's auc: 0.660567 valid_0's binary_logloss: 0.0214766
[4] valid_0's auc: 0.847699 valid_0's binary_logloss: 0.0146109
[5] valid_0's auc: 0.838775 valid_0's binary_logloss: 0.0252176
[6] valid_0's auc: 0.839122 valid_0's binary_logloss: 0.0191823
[7] valid_0's auc: 0.837369 valid_0's binary_logloss: 0.01829
[8] valid_0's auc: 0.828801 valid_0's binary_logloss: 0.0188107
[9] valid_0's auc: 0.829557 valid_0's binary_logloss: 0.0195046
[10] valid_0's auc: 0.811758 valid_0's binary_logloss: 0.0205142
[11] valid_0's auc: 0.811364 valid_0's binary_logloss: 0.022583
[12] valid_0's auc: 0.766871 valid_0's binary_logloss: 0.0228871
[13] valid_0's auc: 0.811503 valid_0's binary_logloss: 0.0215574
[14] valid_0's auc: 0.814388 valid_0's binary_logloss: 0.0246988
[15] valid_0's auc: 0.805495 valid_0's binary_logloss: 0.0282179
[16] valid_0's auc: 0.805208 valid_0's binary_logloss: 0.0286174
[17] valid_0's auc: 0.807372 valid_0's binary_logloss: 0.0279136
[18] valid_0's auc: 0.810976 valid_0's binary_logloss: 0.0243398
[19] valid_0's auc: 0.816831 valid_0's binary_logloss: 0.0241958
[20] valid_0's auc: 0.816681 valid_0's binary_logloss: 0.0246229
[21] valid_0's auc: 0.816423 valid_0's binary_logloss: 0.0241755
[22] valid_0's auc: 0.814858 valid_0's binary_logloss: 0.0260238
[23] valid_0's auc: 0.600747 valid_0's binary_logloss: 0.0363027
[24] valid_0's auc: 0.619092 valid_0's binary_logloss: 0.0352866
[25] valid_0's auc: 0.807625 valid_0's binary_logloss: 0.0330898
[26] valid_0's auc: 0.759556 valid_0's binary_logloss: 0.033595
[27] valid_0's auc: 0.878665 valid_0's binary_logloss: 0.0311388
[28] valid_0's auc: 0.788262 valid_0's binary_logloss: 0.0317903
[29] valid_0's auc: 0.779519 valid_0's binary_logloss: 0.0288819
[30] valid_0's auc: 0.779187 valid_0's binary_logloss: 0.0289138
[31] valid_0's auc: 0.78883 valid_0's binary_logloss: 0.0305115
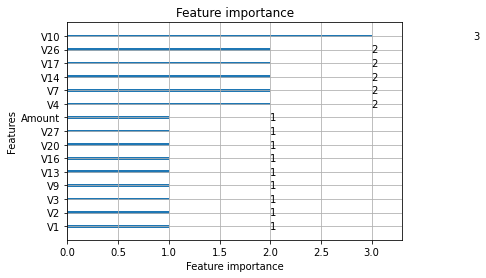
내가 진행한 것 요약
- lightGBM 사용하였으며 초기에 빠른 하이퍼 파라미터 값 지정을 위해 n_estimator = 100으로 설정
- 여러가지 과적합 방지용 하이퍼 파라미터가 존재하나 max_depth 이외에는 어떤 값을 후보군(GridSearch 진행할 때)으로 넣으면 좋을지 기준을 몰라서 max_depth만 진행
- GridSearchCV의 cv=3, early_stopping_rounds = 30, eval_set = ([X_test, y_test]), eval_metric = ‘auc’ 로 두고 진행
- lightgbm 자체 내장함수인 plot_importances 함수 활용해서 feature importances 그래프 출력
아래 책에서 진행한 부분을 통한 피드백
- roc_auc_score 함수에는 y_test, preds를 주는게 아니라 y_test, probs를 줘야함
지금부터는 책에서 진행된 부분
짚으면 좋을 부분
- Amount 칼럼의 데이터 분포가 불균형하기 때문에 StandardScaler 이후 log를 취해줌 (아래에서 좀 더 설명)
- 이상치(Outlier)를 찾는 방법과 이를 제거할 수 있는 방법을 알려줌
- Smote를 통해 불균형 레이블들의 비율을 균등하게 맞추고 성능을 도출함
- 그러나 여기 예시에선 성능이 딱히 향상되지는 않았음(재현율이 오른만큼 정밀도가 떨어졌음)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
%matplotlib inline
card_df = pd.read_csv('./creditcard.csv')
card_df.head(3)
| Time | V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | V10 | V11 | V12 | V13 | V14 | V15 | V16 | V17 | V18 | V19 | V20 | V21 | V22 | V23 | V24 | V25 | V26 | V27 | V28 | Amount | Class | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | -1.359807 | -0.072781 | 2.536347 | 1.378155 | -0.338321 | 0.462388 | 0.239599 | 0.098698 | 0.363787 | 0.090794 | -0.551600 | -0.617801 | -0.991390 | -0.311169 | 1.468177 | -0.470401 | 0.207971 | 0.025791 | 0.403993 | 0.251412 | -0.018307 | 0.277838 | -0.110474 | 0.066928 | 0.128539 | -0.189115 | 0.133558 | -0.021053 | 149.62 | 0 |
| 1 | 0.0 | 1.191857 | 0.266151 | 0.166480 | 0.448154 | 0.060018 | -0.082361 | -0.078803 | 0.085102 | -0.255425 | -0.166974 | 1.612727 | 1.065235 | 0.489095 | -0.143772 | 0.635558 | 0.463917 | -0.114805 | -0.183361 | -0.145783 | -0.069083 | -0.225775 | -0.638672 | 0.101288 | -0.339846 | 0.167170 | 0.125895 | -0.008983 | 0.014724 | 2.69 | 0 |
| 2 | 1.0 | -1.358354 | -1.340163 | 1.773209 | 0.379780 | -0.503198 | 1.800499 | 0.791461 | 0.247676 | -1.514654 | 0.207643 | 0.624501 | 0.066084 | 0.717293 | -0.165946 | 2.345865 | -2.890083 | 1.109969 | -0.121359 | -2.261857 | 0.524980 | 0.247998 | 0.771679 | 0.909412 | -0.689281 | -0.327642 | -0.139097 | -0.055353 | -0.059752 | 378.66 | 0 |
from sklearn.model_selection import train_test_split
# 인자로 입력받은 DataFrame을 복사 한 뒤 Time 컬럼만 삭제하고 복사된 DataFrame 반환
def get_preprocessed_df(df=None):
df_copy = df.copy()
df_copy.drop('Time', axis=1, inplace=True)
return df_copy
# 사전 데이터 가공 후 학습과 테스트 데이터 세트를 반환하는 함수.
def get_train_test_dataset(df=None):
# 인자로 입력된 DataFrame의 사전 데이터 가공이 완료된 복사 DataFrame 반환
df_copy = get_preprocessed_df(df)
# DataFrame의 맨 마지막 컬럼이 레이블, 나머지는 피처들
X_features = df_copy.iloc[:, :-1]
y_target = df_copy.iloc[:, -1]
# train_test_split( )으로 학습과 테스트 데이터 분할. stratify=y_target으로 Stratified 기반 분할
X_train, X_test, y_train, y_test = \
train_test_split(X_features, y_target, test_size=0.3, random_state=0, stratify=y_target)
# 학습과 테스트 데이터 세트 반환
return X_train, X_test, y_train, y_test
X_train, X_test, y_train, y_test = get_train_test_dataset(card_df)
print('학습 데이터 레이블 값 비율')
print(y_train.value_counts()/y_train.shape[0] * 100)
print('테스트 데이터 레이블 값 비율')
print(y_test.value_counts()/y_test.shape[0] * 100)
학습 데이터 레이블 값 비율
0 99.827451
1 0.172549
Name: Class, dtype: float64
테스트 데이터 레이블 값 비율
0 99.826785
1 0.173215
Name: Class, dtype: float64
from sklearn.metrics import confusion_matrix, accuracy_score, precision_score, recall_score, f1_score
from sklearn.metrics import roc_auc_score
def get_clf_eval(y_test, pred=None, pred_proba=None):
confusion = confusion_matrix( y_test, pred)
accuracy = accuracy_score(y_test , pred)
precision = precision_score(y_test , pred)
recall = recall_score(y_test , pred)
f1 = f1_score(y_test,pred)
# ROC-AUC 추가
roc_auc = roc_auc_score(y_test, pred_proba)
print('오차 행렬')
print(confusion)
# ROC-AUC print 추가
print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f},\
F1: {3:.4f}, AUC:{4:.4f}'.format(accuracy, precision, recall, f1, roc_auc))
from sklearn.linear_model import LogisticRegression
lr_clf = LogisticRegression()
lr_clf.fit(X_train, y_train)
lr_pred = lr_clf.predict(X_test)
lr_pred_proba = lr_clf.predict_proba(X_test)[:, 1]
# 3장에서 사용한 get_clf_eval() 함수를 이용하여 평가 수행.
get_clf_eval(y_test, lr_pred, lr_pred_proba)
오차 행렬
[[85279 16]
[ 58 90]]
정확도: 0.9991, 정밀도: 0.8491, 재현율: 0.6081, F1: 0.7087, AUC:0.9589
# 인자로 사이킷런의 Estimator객체와, 학습/테스트 데이터 세트를 입력 받아서 학습/예측/평가 수행.
def get_model_train_eval(model, ftr_train=None, ftr_test=None, tgt_train=None, tgt_test=None):
model.fit(ftr_train, tgt_train)
pred = model.predict(ftr_test)
pred_proba = model.predict_proba(ftr_test)[:, 1]
get_clf_eval(tgt_test, pred, pred_proba)
from lightgbm import LGBMClassifier
lgbm_clf = LGBMClassifier(n_estimators=1000, num_leaves=64, n_jobs=-1, boost_from_average=False)
get_model_train_eval(lgbm_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train, tgt_test=y_test)
오차 행렬
[[85290 5]
[ 36 112]]
정확도: 0.9995, 정밀도: 0.9573, 재현율: 0.7568, F1: 0.8453, AUC:0.9790
데이터 분포도 변환 후 모델 학습/예측/평가
import seaborn as sns
plt.figure(figsize=(8, 4))
plt.xticks(range(0, 30000, 1000), rotation=60) # x축의 글자를 60도 회전시킴
sns.distplot(card_df['Amount']) # 27,000불 까지 드물지만 사용한 내역이 있어서 꼬리가 긴 형태의 분포 곡선을 가지는 걸 볼 수 있음
# sns.displot(card_df['Amount'])
# sns.histplot(card_df['Amount'])
<AxesSubplot:xlabel='Amount', ylabel='Density'>

from sklearn.preprocessing import StandardScaler
# 사이킷런의 StandardScaler를 이용하여 정규분포 형태로 Amount 피처값 변환하는 로직으로 수정.
def get_preprocessed_df(df=None):
df_copy = df.copy()
scaler = StandardScaler()
amount_n = scaler.fit_transform(df_copy['Amount'].values.reshape(-1, 1))
# 변환된 Amount를 Amount_Scaled로 피처명 변경후 DataFrame맨 앞 컬럼으로 입력
df_copy.insert(0, 'Amount_Scaled', amount_n)
# 기존 Time, Amount 피처 삭제
df_copy.drop(['Time','Amount'], axis=1, inplace=True)
return df_copy
# Amount를 정규분포 형태로 변환 후 로지스틱 회귀 및 LightGBM 수행.
X_train, X_test, y_train, y_test = get_train_test_dataset(card_df)
print('### 로지스틱 회귀 예측 성능 ###')
lr_clf = LogisticRegression()
get_model_train_eval(lr_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train, tgt_test=y_test)
print('### LightGBM 예측 성능 ###')
lgbm_clf = LGBMClassifier(n_estimators=1000, num_leaves=64, n_jobs=-1, boost_from_average=False)
get_model_train_eval(lgbm_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train, tgt_test=y_test)
### 로지스틱 회귀 예측 성능 ###
오차 행렬
[[85281 14]
[ 58 90]]
정확도: 0.9992, 정밀도: 0.8654, 재현율: 0.6081, F1: 0.7143, AUC:0.9707
### LightGBM 예측 성능 ###
오차 행렬
[[85289 6]
[ 36 112]]
정확도: 0.9995, 정밀도: 0.9492, 재현율: 0.7568, F1: 0.8421, AUC:0.9773
- 불균형한 데이터 분포를 가지고 있는 ‘Amount’ 값에 log 값으로 변환시킴
- 원본의 큰 값을 상대적으로 작은 값으로 변환하기 때문에 데이터 분포도 왜곡을 상당수준 개선시켜줌
def get_preprocessed_df(df=None):
df_copy = df.copy()
# 넘파이의 log1p( )를 이용하여 Amount를 로그 변환
amount_n = np.log1p(df_copy['Amount'])
df_copy.insert(0, 'Amount_Scaled', amount_n)
df_copy.drop(['Time','Amount'], axis=1, inplace=True)
return df_copy
X_train, X_test, y_train, y_test = get_train_test_dataset(card_df)
print('### 로지스틱 회귀 예측 성능 ###')
get_model_train_eval(lr_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train, tgt_test=y_test)
print('### LightGBM 예측 성능 ###')
get_model_train_eval(lgbm_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train, tgt_test=y_test)
### 로지스틱 회귀 예측 성능 ###
오차 행렬
[[85283 12]
[ 59 89]]
정확도: 0.9992, 정밀도: 0.8812, 재현율: 0.6014, F1: 0.7149, AUC:0.9727
### LightGBM 예측 성능 ###
오차 행렬
[[85290 5]
[ 35 113]]
정확도: 0.9995, 정밀도: 0.9576, 재현율: 0.7635, F1: 0.8496, AUC:0.9796
- 성능이 어느정도 개선되었음을 확인함
이상치 데이터 제거 후 모델 학습/예측/평가
- 어떤 컬럼에 대해서 이상치 제거작업을 할지 정해야 함. 즉 전체 칼럼에 대해서 시각화하고, 어떤 칼럼에 대해 이상치 작업을 할지 골라보자
import seaborn as sns
plt.figure(figsize=(9, 9))
corr = card_df.corr()
sns.heatmap(corr, cmap='RdBu')
<AxesSubplot:>
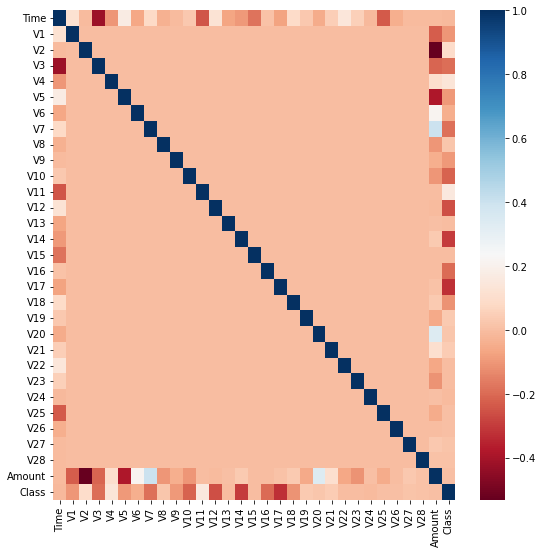
- 문제에서 가장 중요한 건 Class를 잘 맞추는것
- Class와 상관관계가 높은 칼럼은 V17가 첫번째, V14가 두번째
- 이 중 V14에 대한 이상치를 제거해보자
- 이상치 제거 방법은 IQR을 통해 진행
- IQR = Q3 - Q1으로 이상치 검출을 위해 적당한 값을 찾는것임. 이 값을 기준으로 + 1.5(Q3), - 1.5(Q1) 처리를 통해 이상치를 검출함
import numpy as np
def get_outlier(df=None, column=None, weight=1.5):
# fraud에 해당하는 column 데이터만 추출, 1/4 분위와 3/4 분위 지점을 np.percentile로 구함.
fraud = df[df['Class']==1][column]
quantile_25 = np.percentile(fraud.values, 25)
quantile_75 = np.percentile(fraud.values, 75)
# IQR을 구하고, IQR에 1.5를 곱하여 최대값과 최소값 지점 구함.
iqr = quantile_75 - quantile_25
iqr_weight = iqr * weight
lowest_val = quantile_25 - iqr_weight
highest_val = quantile_75 + iqr_weight
# 최대값 보다 크거나, 최소값 보다 작은 값을 아웃라이어로 설정하고 DataFrame index 반환.
outlier_index = fraud[(fraud < lowest_val) | (fraud > highest_val)].index
return outlier_index
outlier_index = get_outlier(df=card_df, column='V14', weight=1.5)
print('이상치 데이터 인덱스:', outlier_index)
이상치 데이터 인덱스: Int64Index([8296, 8615, 9035, 9252], dtype='int64')
# get_processed_df( )를 로그 변환 후 V14 피처의 이상치 데이터를 삭제하는 로직으로 변경.
def get_preprocessed_df(df=None):
df_copy = df.copy()
amount_n = np.log1p(df_copy['Amount'])
df_copy.insert(0, 'Amount_Scaled', amount_n)
df_copy.drop(['Time','Amount'], axis=1, inplace=True)
# 이상치 데이터 삭제하는 로직 추가
outlier_index = get_outlier(df=df_copy, column='V14', weight=1.5)
df_copy.drop(outlier_index, axis=0, inplace=True)
return df_copy
X_train, X_test, y_train, y_test = get_train_test_dataset(card_df)
print('### 로지스틱 회귀 예측 성능 ###')
get_model_train_eval(lr_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train, tgt_test=y_test)
print('### LightGBM 예측 성능 ###')
get_model_train_eval(lgbm_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train, tgt_test=y_test)
### 로지스틱 회귀 예측 성능 ###
오차 행렬
[[85282 13]
[ 48 98]]
정확도: 0.9993, 정밀도: 0.8829, 재현율: 0.6712, F1: 0.7626, AUC:0.9747
### LightGBM 예측 성능 ###
오차 행렬
[[85291 4]
[ 25 121]]
정확도: 0.9997, 정밀도: 0.9680, 재현율: 0.8288, F1: 0.8930, AUC:0.9831
SMOTE 오버 샘플링 적용 후 모델 학습/예측/평가
from imblearn.over_sampling import SMOTE
smote = SMOTE(random_state=0)
# X_train_over, y_train_over = smote.fit_sample(X_train, y_train) 이 코드가 작동을 안해서 resample()로 대체.
X_train_over, y_train_over = smote.fit_resample(X_train, y_train)
print('SMOTE 적용 전 학습용 피처/레이블 데이터 세트: ', X_train.shape, y_train.shape)
print('SMOTE 적용 후 학습용 피처/레이블 데이터 세트: ', X_train_over.shape, y_train_over.shape)
print('SMOTE 적용 전 레이블 값 분포: \n', pd.Series(y_train).value_counts())
print('SMOTE 적용 후 레이블 값 분포: \n', pd.Series(y_train_over).value_counts())
SMOTE 적용 전 학습용 피처/레이블 데이터 세트: (199364, 29) (199364,)
SMOTE 적용 후 학습용 피처/레이블 데이터 세트: (398040, 29) (398040,)
SMOTE 적용 전 레이블 값 분포:
0 199020
1 344
Name: Class, dtype: int64
SMOTE 적용 후 레이블 값 분포:
0 199020
1 199020
Name: Class, dtype: int64
lr_clf = LogisticRegression()
# ftr_train과 tgt_train 인자값이 SMOTE 증식된 X_train_over와 y_train_over로 변경됨에 유의
get_model_train_eval(lr_clf, ftr_train=X_train_over, ftr_test=X_test, tgt_train=y_train_over, tgt_test=y_test)
오차 행렬
[[83317 1978]
[ 15 133]]
정확도: 0.9767, 정밀도: 0.0630, 재현율: 0.8986, F1: 0.1178, AUC:0.9803
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
from sklearn.metrics import precision_recall_curve
%matplotlib inline
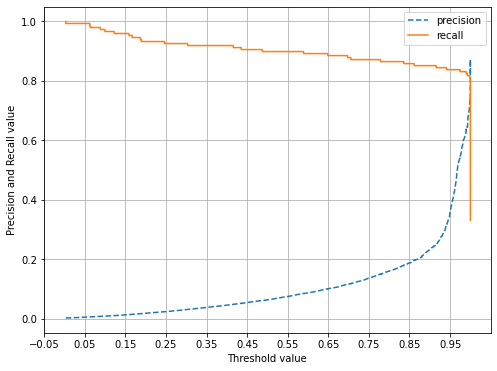
def precision_recall_curve_plot(y_test , pred_proba_c1):
# threshold ndarray와 이 threshold에 따른 정밀도, 재현율 ndarray 추출.
precisions, recalls, thresholds = precision_recall_curve( y_test, pred_proba_c1)
# X축을 threshold값으로, Y축은 정밀도, 재현율 값으로 각각 Plot 수행. 정밀도는 점선으로 표시
plt.figure(figsize=(8,6))
threshold_boundary = thresholds.shape[0]
plt.plot(thresholds, precisions[0:threshold_boundary], linestyle='--', label='precision')
plt.plot(thresholds, recalls[0:threshold_boundary],label='recall')
# threshold 값 X 축의 Scale을 0.1 단위로 변경
start, end = plt.xlim() # xlim으로 초기값, 끝값을 start, end 변수에 넣음
plt.xticks(np.round(np.arange(start, end, 0.1),2))
# x축, y축 label과 legend, 그리고 grid 설정
plt.xlabel('Threshold value'); plt.ylabel('Precision and Recall value')
plt.legend(); plt.grid()
plt.show()
precision_recall_curve_plot( y_test, lr_clf.predict_proba(X_test)[:, 1] )
-0.04679899815285934
1.0498475713406124
lgbm_clf = LGBMClassifier(n_estimators=1000, num_leaves=64, n_jobs=-1, boost_from_average=False)
get_model_train_eval(lgbm_clf, ftr_train=X_train_over, ftr_test=X_test,
tgt_train=y_train_over, tgt_test=y_test)
오차 행렬
[[85286 9]
[ 22 124]]
정확도: 0.9996, 정밀도: 0.9323, 재현율: 0.8493, F1: 0.8889, AUC:0.9789
PREVIOUS경제