기본 개념

• 차원축소의 종류는 2가지
  1. 피처 선택(Feature selection)
     • 다른 피처에 종속성이 강한 피처는 제거하고, 중요한 피처만 남기는 것
  2. 피처 추출(Feature extraction)
     • 기존의 피처들을 압축해서 함축적인 의미를 가지는 새로운 피처로 만드는 것

이해를 위해 선행되어야 하는 개념

PCA 저격용 선형대수 지식

모델

PCA

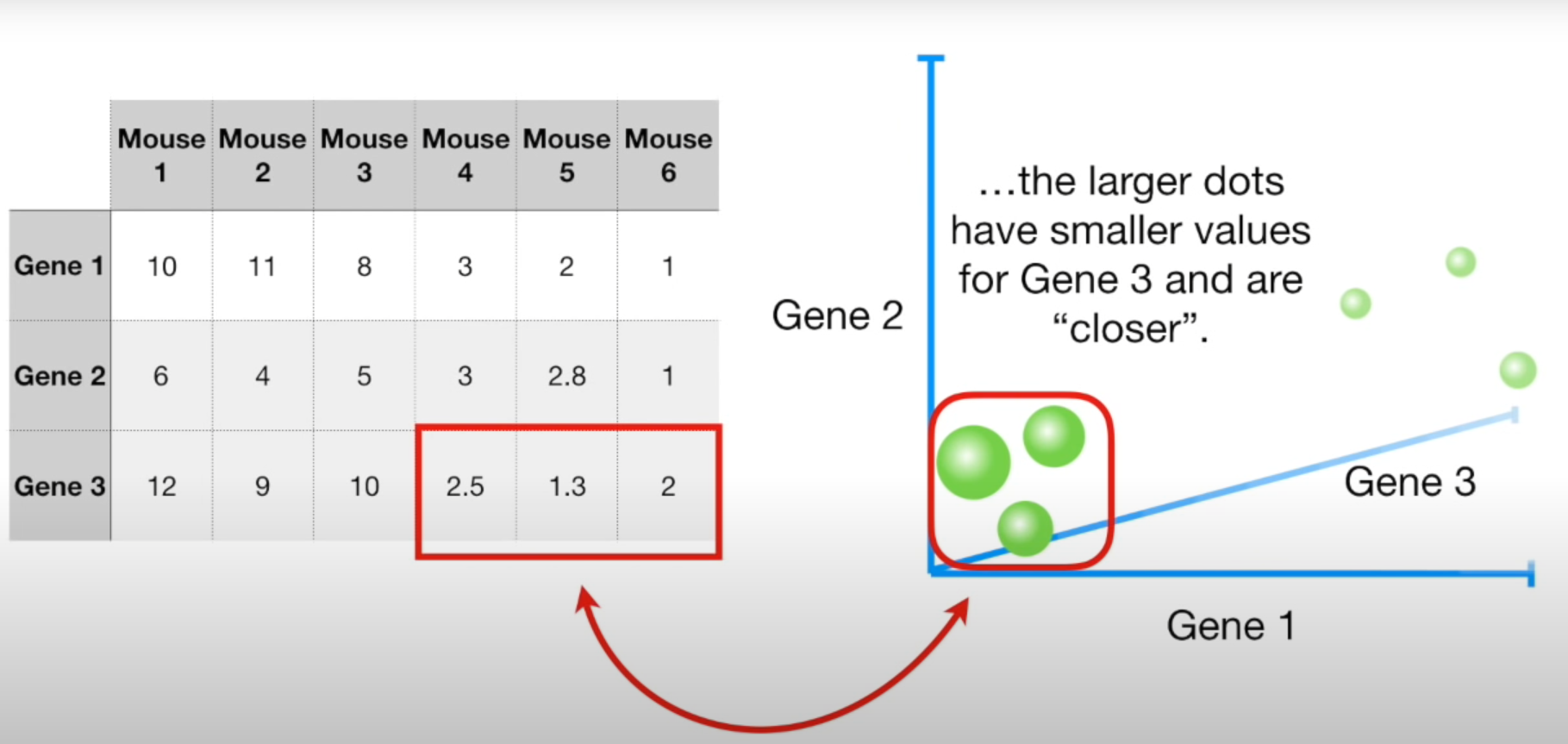
• 3개의 Gene 축을 사용하면 위와같이 표현할 수 있다.
• 더 많은 Gene 축을 활용하면 시각화가 불가능함. PCA를 통해 차원축소가 가능

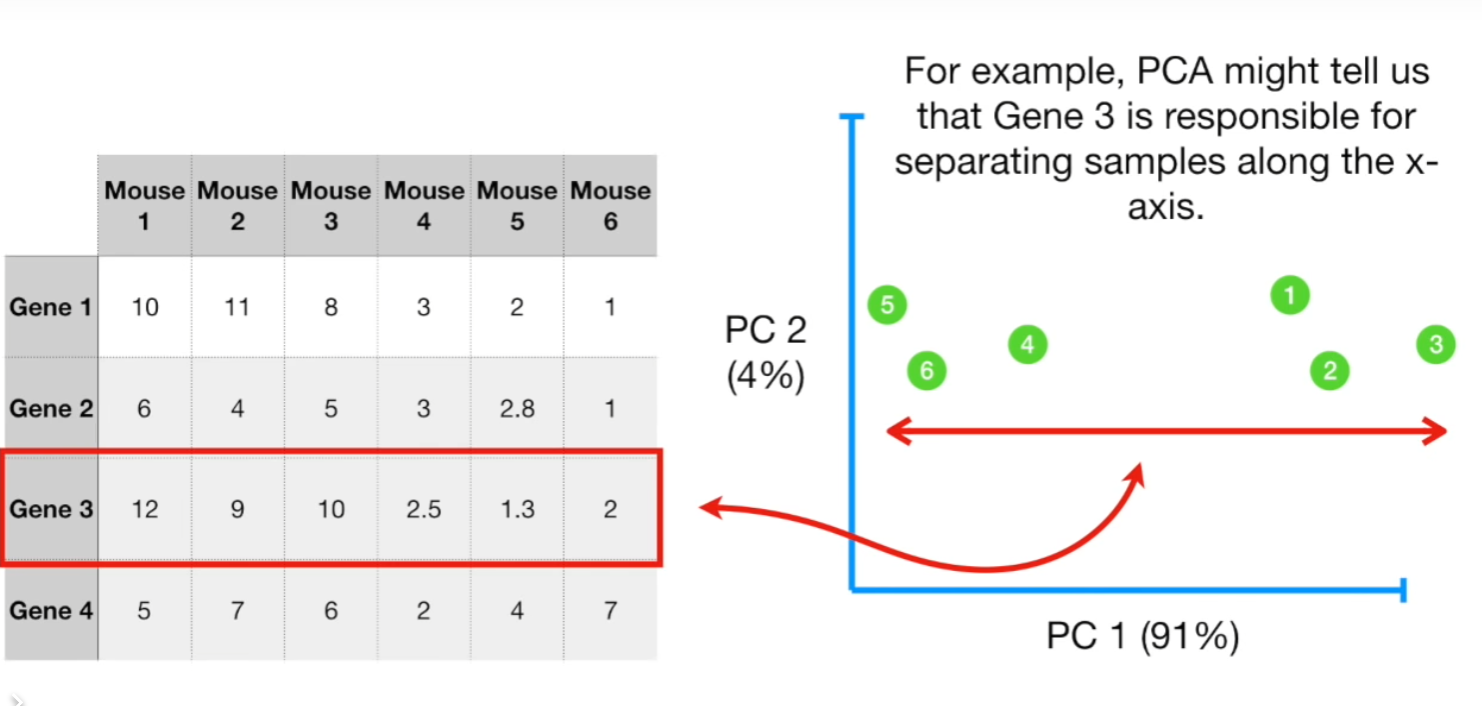
• PCA를 통해 가장 Clustering 하는데 도움을 주는 축을 선정할 수도 있다. 위 그림상에 따르면 Gene 3임
• Gene 3는 x-axis에 대해서 Sample들을 분리시킬 수 있다 → 이런 특성을 뽑을 수 있게 해주는것이 PCA 작업

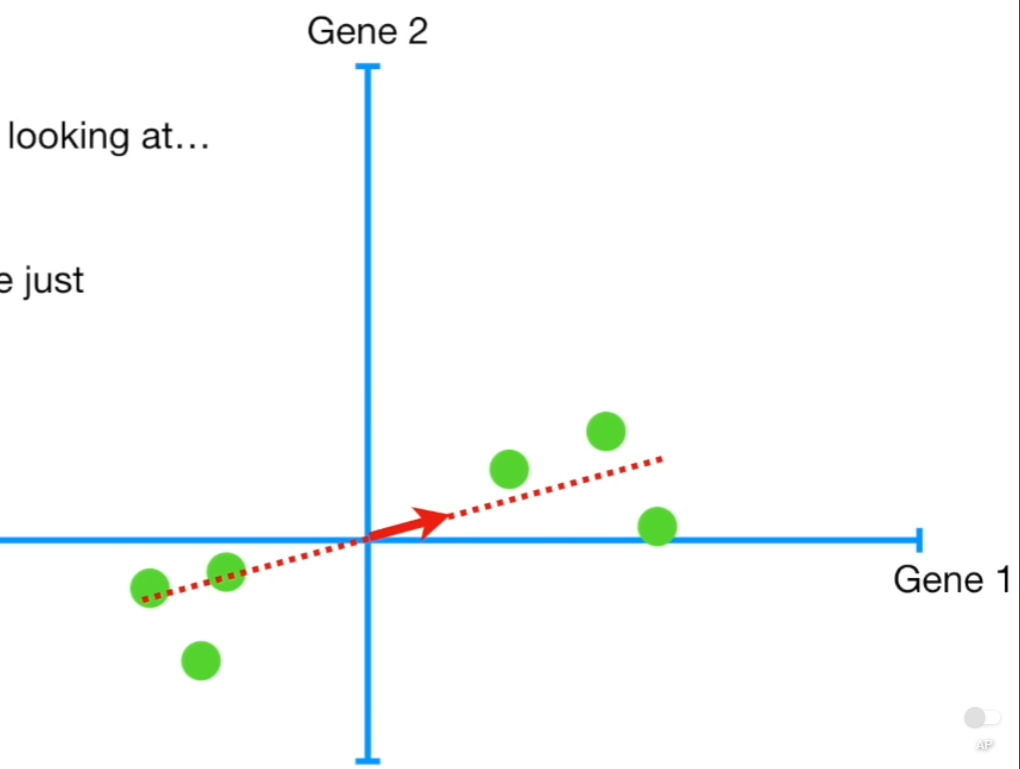
• 위 그림상의 데이터를 가장 잘 반영하는 선을 그을 것이며, 이 선이 잘 그어진 것인지 PCA기법으로 판단할 것임
  • 선이 잘 그어졌는지 판단하기 위한 방 법은 2가지 존재
    1. 데이터와 예측값의 거리(Distance)의 합을 보거나
    2. 데이터를 선에 투영(Projection)했을 때 원점과의 거리를 보면됨. 이때 거리가 길 수록 선이 잘 그어진 것
       1. 모든 데이터에 대해 위 그림처럼 빨간색 선에 투영한 뒤, 그 투영된 점과 원점사이의 거리값을 구해서 다 더해주면 됨
       2. 원점에서 멀 수록 잘 군집화 된것으로 보면 됨.(2개 클래스를 군집화한다고 할 때 서로 거리가 멀어야 잘 군집화된것)
  • PCA는 위 방법중 2번을 택함. 그리고 여기서 SVD를 통해 빨간색 화살표의 길이를 1로 스케일링함
• 빨간선이 PC1(Principal compoent 1)이 됨.
  • PC1에 대해서는 Gene1 쪽으로 4칸 이동할 때 Gene2 쪽으로 1칸 이동하므로 Gene1이 더 중요한 feature임
    • 아직 왜 Gene1이 중요한지 직관적으로 이해는 안됨

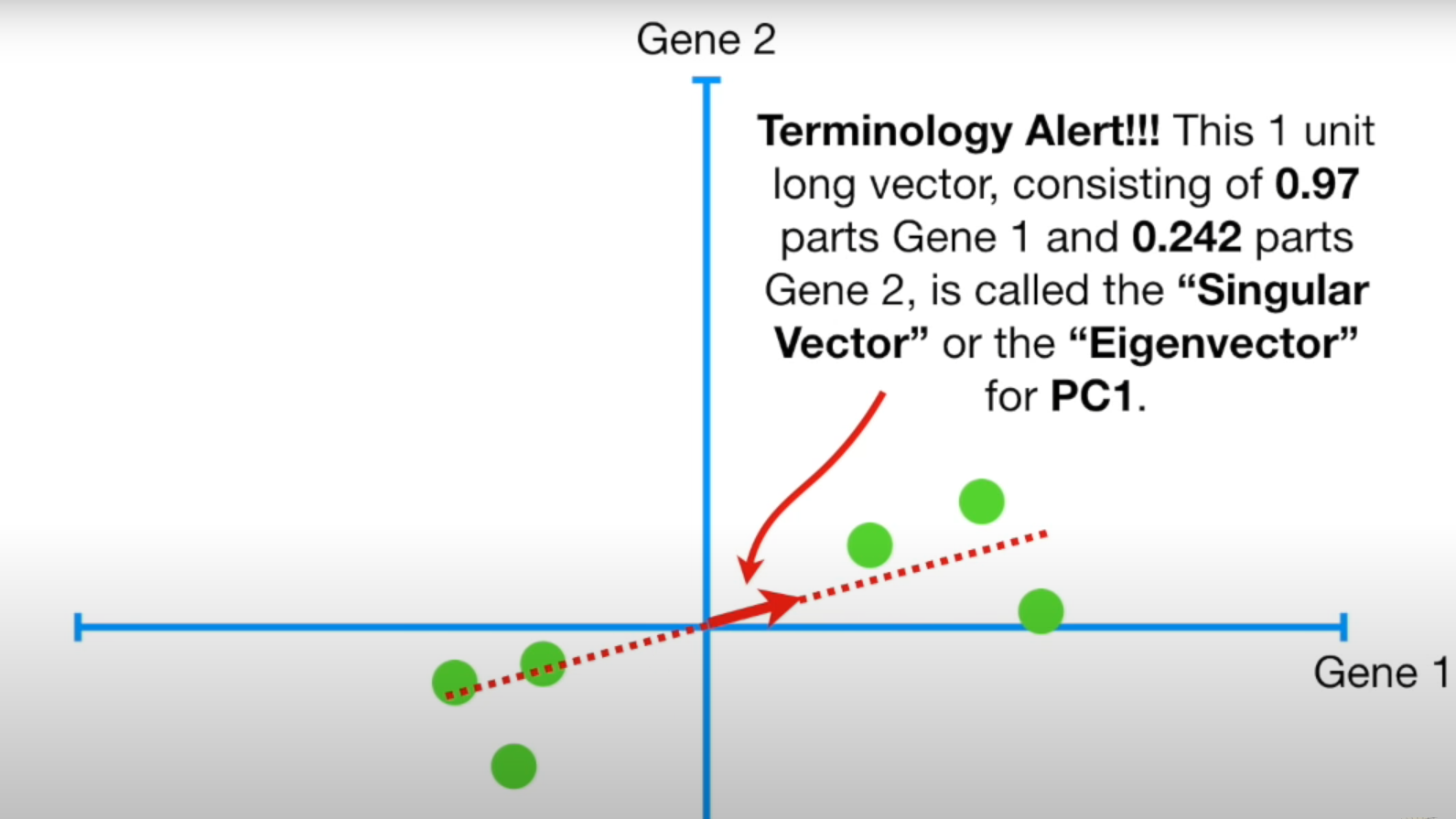
• 스케일링으로 구한 빨간색 유닛벡터가 (0.97, 0.242) 일 때 이게 Singular Vector 혹은 Eigen Vector라고 불림
• 이때의 SS 값을 PC1에 대한 Eigen Value 라고 부름
• $\sqrt{Eigenvalue}$ = Singular Value

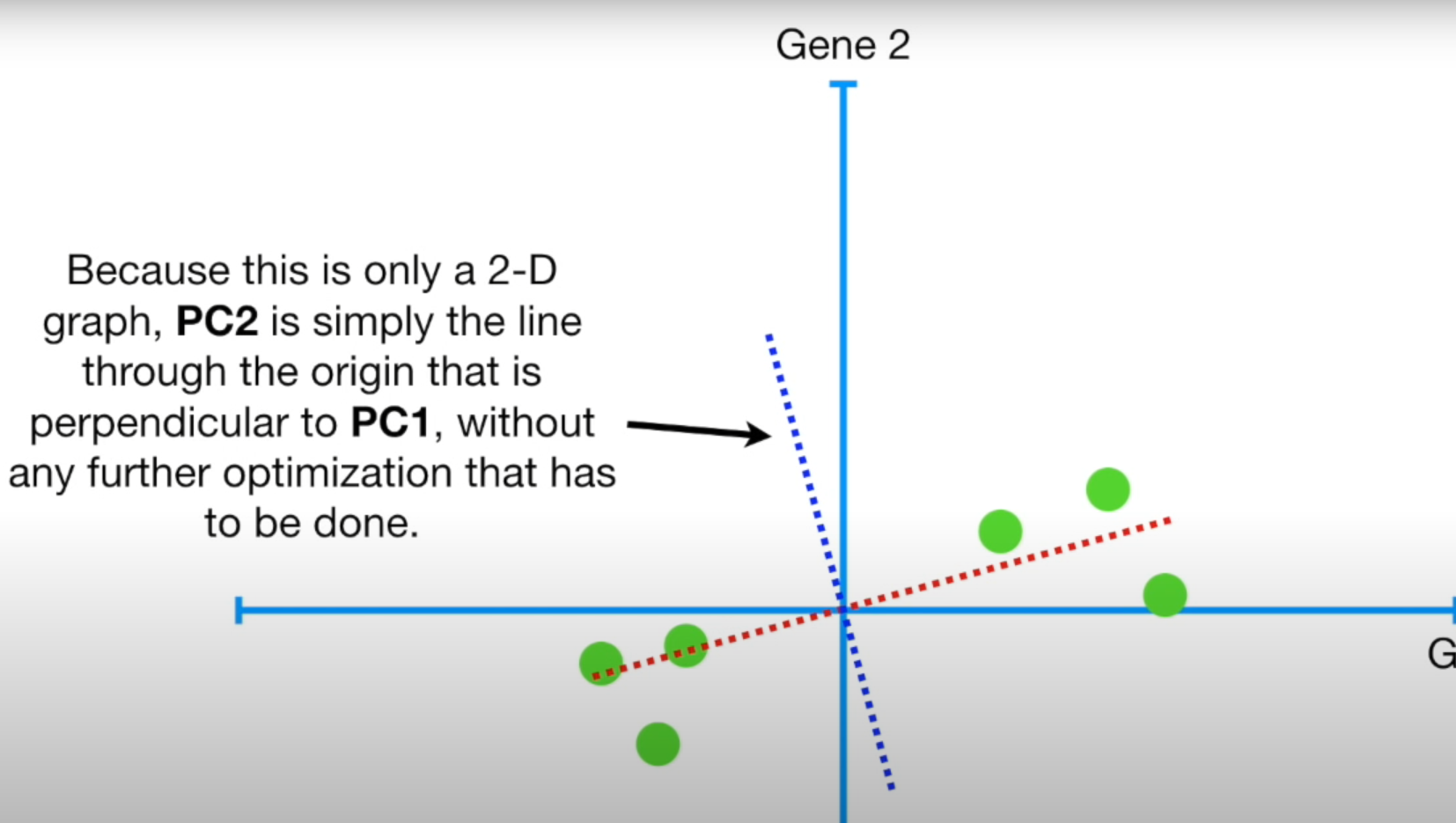
• PC2는 PC1에 수직임 (와우..)
  • PC2에 대해서는 Gene 2가 4배 더 중요함

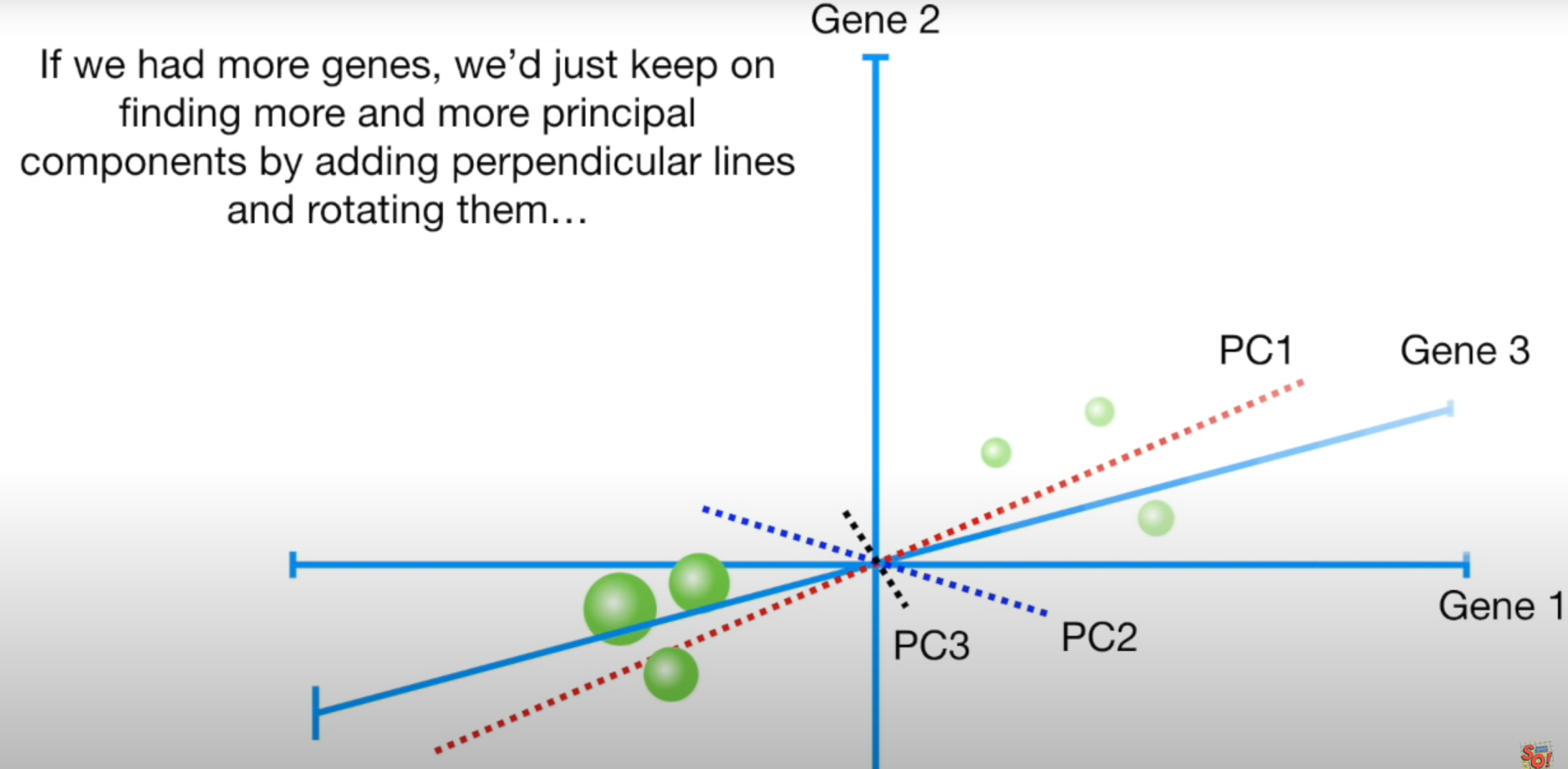
• 3개의 feature에 대해서도 같은 방식으로 적용 가능
  • PC2를 구할 땐 PC1에 수직이면서(PC1에 수직인 직선이 무수히 많음) SS가 최소가 되는 PC2를 찾아야함
  • PC3는 두 선에 수직인 선이므로 바로 나옴

• 여러개의 PC 선들중 중요도를 SS를 통해 구할 수 있음
  • 위 그림에선 2-d 그래프에서 데이터를 표현하고자 한다면 PC1, PC2를 쓰는게 좋은것

입력 데이터의 공분산 행렬이 고유벡터와 고유값으로 분해될 수 있으며, 이렇게 분해된 고유벡터를 이용해 입력 데이터를 선형 변환하는 방식이 PCA

• 내가 유튜브로 공부한 부분은 데이터를 통해서 PCA 진행하는 과정 배운것인데 파이썬 머신러닝 완벽가이드 서적에서는 공분산 행렬을 통해 PCA 진행함. 이 둘을 연관짓는건 추후에 진행해 볼 예정