기본 개념
핵심은 중복되는 연산을 줄이자
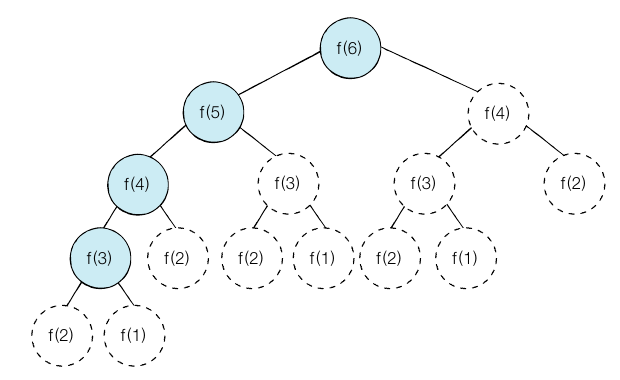
피보나치 그림 예시
원래는 흰색 노드 값들도 모두 계산해야줘야 하지만
한번 계산이 끝난 값들을 메모리에 저장해두고 재사용하여 중복 연산을 줄인다.
- 다이나믹 프로그래밍으로 해결한다는 말의 의미: 큰 문제를 작게 나누고, 같은 문제면 한 번씩만 풀어 문제를 효율적으로 해결하자
- 어디서나 적용 가능한 것은 아니며 다음 2가지 조건을 만족해야함
- 큰 문제를 작은 문제로 나눌 수 있다.
- 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일하다.
피보나치 문제의 점화식은 다음과 같다.
$F_1 = 1, F_2 = 1$
$F_n = F_{n-1} + F_{n-2}$
-
재귀 함수를 통해 구현하면 처음 그래프 그림 예시가 된다.
def fibo(x): if x==1 or x==2: return 1 return fibo(x - 1) + fibo(x - 2) print(fibo(4)) -
재귀 함수를 통한 메모이제이션 기법 적용한 피보나치 수열 구현(메모이제이션: 구한 결과를 메모리 공간에 메모해두고 같은 식을 다시 호출하면 메모한 결과를 그대로 가져오는 기법)
# 한번 계산된 결과를 메모이제이션(Memoization)하기 위한 리스트 초기화 d = [0] * 100 # 피보나치 함수(Fibonacci Function)를 재귀적으로 구현(탑다운 다이나믹 프로그래밍) def fibo(x): # 종료 조건(1 혹은 2일 때 1을 반환) if x==1 or x==2: return 1 # 이미 계산한 적 있는 문제라면 그대로 반환 if d[x] != 0: return d[x] # 아직 계산하지 않았다면 메모리에 저장하고 계산된 값 반환 result = fibo(x-1) + fibo(x-2) d[x] = result return result print(fibo(99)) -
반복문을 통한 DP 테이블 기법 적용한 피보나치 수열
# 앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화 d = [0] * 100 # 첫 번째 피보나치 수와 두 번째 피보나치 수는 1 d[1] = 1 d[2] = 1 def fibo(n): for i in range(3, n + 1): d[i] = d[i - 1] + d[i - 2] return d[n] print(fibo(8))
재귀 함수를 통해 다이나믹 프로그래밍을 구현하는것을 탑다운(하향식) 방법이라고 하며, 위에서 메모이제이션 개념을 통해 계산한 값을 재사용 하였음을 보였다.
반면 반복문을 통해 다이나믹 프로그래밍을 구현하는것을 바텀업(상향식) 방법이라고 하며, DP 테이블 개념을 통해 계산된 값을 저장 하였음을 보였다.
DP 테이블은 재사용의 개념이 아니다. 또한 재귀함수 깊이 오류로 인해 에러가 날 수 있기 때문에 가능하다면 바텀업 방식을 사용하는것이 권장된다.
문제
p.217
- 내 풀이
x = int(input())
cnt = 0
while True:
if x == 1:
break
if x == 2:
x /= 2
cnt += 1
if x == 3:
x /= 3
cnt += 1
if x == 4:
x /= 2
cnt += 1
if x % 5 != 0:
x -= 1
cnt += 1
else:
x /= 5
cnt += 1
print(cnt)
답안은 맞게 풀었지만 비효율적으로 코드를 짠 느낌이 있다. DP 문제이지만 전혀 DP 처럼 풀지 못했다.
DP 처럼 풀기 위해서는 다음의 2가지가 필요하다.
- 큰 Task를 반복성이 있는 작은 Task로 나눈다.
- 작은 task에서 이미 계산된 것은 또 같은 계산 process를 진행하지 않고 결과값만 사용한다. (중복제거)
- 모범 풀이
x = int(input())
d = [0] * 30001
for i in range(2, x+1):
d[i] = d[i-1] + 1
if i % 2 == 0:
d[i] = min(d[i], d[i // 2] + 1)
if i % 3 == 0:
d[i] = min(d[i], d[i // 3] + 1)
if i % 5 == 0:
d[i] = min(d[i], d[i // 5] + 1)
print(d[x])
전날 위 모범답안을 보면서 이해하고 다음날 다시 풀어봤는데 제대로 풀지 못했다. 이해를 잘 하지 못한것이다. 다음의 포인트들 때문에 전날과 다른 출력 결과가 나왔었다.
if i % 2 == 0:
d[i] = min(d[i], d[i // 2]) # 맨 처음 d[i] = d[i-1] + 1 을 통해 현재 진행중인 연산 카운팅을 해주므로
# if문 3곳에서는 + 1 을 해줄 필요가 없을 것이라 생각함
if i % 3 == 0:
d[i] = min(d[i], d[i // 3])
if i % 5 == 0:
d[i] = min(d[i], d[i // 5])
논리적인 사고력이 부족해서 발생하는 문제로 보인다 ㅋㅋㅋ… ㅜㅜㅜㅜ
다음을 중시해야 한다.
- 맨 처음
d[i] = d[i-1] + 1을 통해 다른 if 문들을 통과하기전 현재의 d[i]는 내가 해야하는 4가지 연산(i-1, i/2, i/3, i/5)중 가장 작은 연산 기록을 가지고 있는것으로 간주하며 (아직 비교는 하지 않았지만 코드 흐름상 그렇게 생각해야함), 이에 따라 + 1 을 통해 마무리 작업을 해준다.
그래서 아래와 같이 코드를 짰지만 역시나 정답 출력결과물과는 달랐다.
x = int(input())
d = [0] * 30001
for i in range(2, x+1):
d[i] = d[i-1] + 1
if i % 2 == 0:
d[i] = min(d[i], d[i // 2]) + 1
if i % 3 == 0:
d[i] = min(d[i], d[i // 3]) + 1
if i % 5 == 0:
d[i] = min(d[i], d[i // 5]) + 1
print(d[x])
if 문에서 두 연산 결과를 비교하여 가장 작은 값을 선정한 이후 맨 처음 d[i] = d[i - 1] + 1 에서 해줬던 것 처럼 + 1 로 마무리 작업을 해준것인데 다음의 문제점들이 발생한다.
- 2, 3, 5 로 모두 나눌 수 있는 경우들을 생각해보면 + 1 이 계속 누적된다. 나는 값이 대체 되는것을 원하므로 for문 한번 돌 때 + 1이 한번만 이루어져야 하지만, for문 한번에 + 4 가 될 수도 있다.
따라서 다음과 같이 코드를 짜야 정답 결과물이 출력된다.
x = int(input())
d = [0] * 30001
for i in range(2, x+1):
d[i] = d[i-1] + 1
if i % 2 == 0:
d[i] = min(d[i], d[i // 2]) + 1
if i % 3 == 0:
d[i] = min(d[i], d[i // 3]) + 1
if i % 5 == 0:
d[i] = min(d[i], d[i // 5]) + 1
print(d[x])
p.220
2개중 전체 문제를 작은 문제로 쪼개서 생각 및 구현까지 완료한 것은 정말 좋았다. 실제로 짝수 갯수로 배열을 채워서 작동시키면 올바르게 작동하는 걸로 보인다.
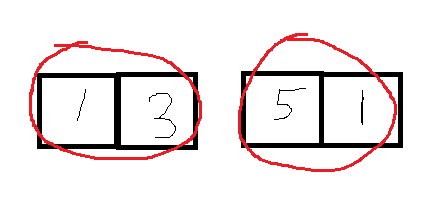
위 그림이 내 아이디어였는데 이 그림의 문제점은 배열 갯수를 짝수로 가정해버리는 것이다. 홀수 갯수로 배열을 채우면 index 에러가 나면서 종료가 되버린다.
N = int(input())
storage = [0] * N
result = 0
val = input().split()
for idx, value in enumerate(val):
storage[idx] = int(value)
idx = 0
temp_idx = []
while(True):
if idx >= N:
break
if storage[idx] >= storage[idx+1]:
temp_idx.append(idx)
elif storage[idx] < storage[idx+1]:
temp_idx.append(idx+1)
# 같은거 처리 어케하지?
else:
print("같은거..")
pass
idx += 2
if idx == 2:
continue
if temp_idx[-1] - temp_idx[-2] == 1: # 붙어있다면..
tp1 = storage[temp_idx[-2] -1] + storage[temp_idx[-1]]
tp2 = storage[temp_idx[-2] -1] + storage[temp_idx[-1] + 1]
tp3 = storage[temp_idx[-2]] + storage[temp_idx[-1] + 1]
max = 0
if tp1 > max:
max = tp1
if tp2 > max:
max = tp2
if tp3 > max:
max = tp3
if max == tp1:
temp_idx[-2] -= 1
elif max == tp2:
temp_idx[-2] -= 1
temp_idx[-1] += 1
else:
temp_idx[-1] += 1
for idx in temp_idx:
result += storage[idx]
print(result)
답안 코드를 이해하기 위해선 아래 말을 완벽히 이해하고 있어야 한다.
DP table에 들어있는 각각의 값들은 그 index에서 최고로 높게 훔친 값이며 각각의 인덱스마다 선택된 경우의 수가 다를 수 있다. 가령 d[3]이 3, 5를 택했다고 해서, d[4]도 무조건 3, 5를 택하고 시작해야 하는 법은 없다.
즉, d[3], d[4]에는 각각 다른 경우의 수가 들어있다. 즉 여러 경우의 수를 서로 비교해가면서 계속 d를 채워나간다.
코드로 구현하기 가장 어려웠던 부분이 d[0], d[1]를 어떻게 처리해줘야 하는지였다. 다음과 같은 마인드 세팅을 했더니 한결 수월해졌다.
d[0]은 숫자가 하나 주워진 것이므로 무조건 택해야 최대값이고, d[1]은 두 숫자가 붙어있기는 하지만 단지 두개의 숫자일 뿐이므로 둘 중 max 값을 고르면 된다.
그럼 d[0], d[1]도 각각의 인덱스(첫번째, 두번째)에서 최대값을 가지고 있는것이 되므로 d[2]부터 본격적으로 \(a_{i} = max(a_{i-1}, a_{i-2} + 현재 창고값)\) 점화식을 적용해서 이어나가면 된다.
p.223
손도 못댔다.. ㅋㅋ;;;;;;;;;;
DP 문제가 굉장히 어색하다.
답안 코드를 보고도 이해를 못해서 나동빈 설명 영상을 보고 간신히 이해하였다…
추가적으로 스스로 이해를 위한 그림을 그려봤다.
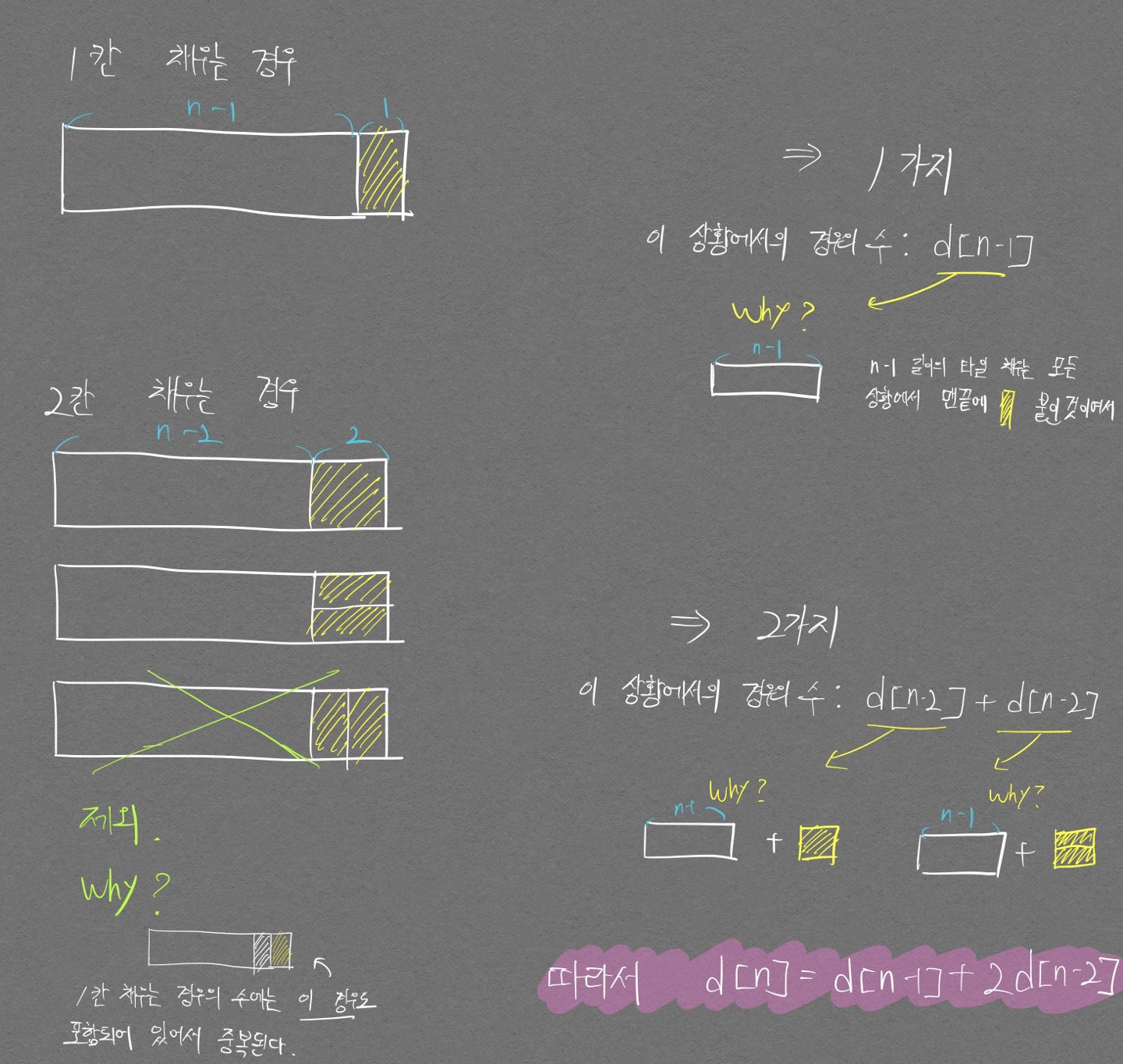
- 답안 코드
n = int(input())
# d = [0] * 1000
d = [0] * 1001
# 1칸 일 때 고려하는것 이므로 d[0]가 아닌 d[1]로 생각하는것이 편하다.
d[1] = 1
d[2] = 3
for i in range(n):
d[i] = (d[i-1] + 2 * d[i-2]) % 796796
print(d[n])