정규 분포

\[f(x) = {1 \over \sqrt{2\pi}\sigma}e^{-(x-m)^2 \over (2\sigma)^2}\]

평균 $ \mu $와 표준편차 $\sigma^2$에 의해 그 분포가 확정된다

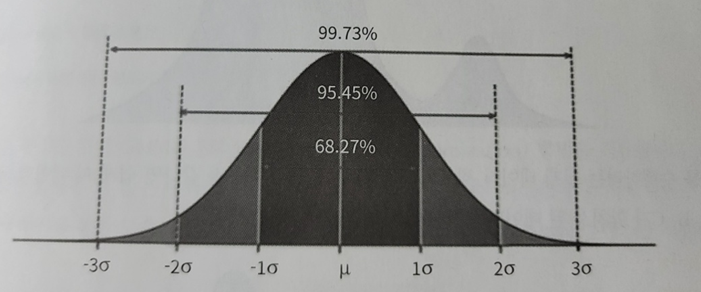
평균값과 분산값을 이용해 구한 범위에서 위와같이 확률이 결정된다.

즉, 평균과 분산을 알면 확률값을 알 수 있다.

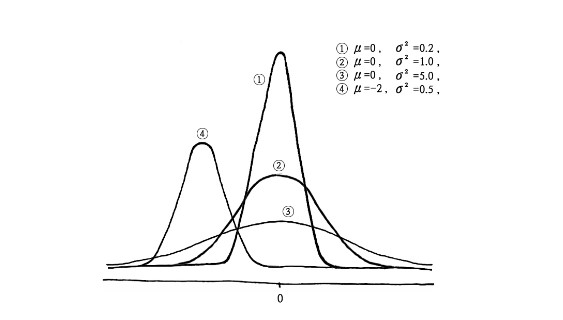
평균, 표준편차가 달라짐에 따라 위 그림과 같이 Gaussian 분포의 모양이 달라진다.
Gaussian blur를 적용하기 위한 fuzzy filter가 있다고 할 때 표준편차가 커지면, fuzzy filter의 크기가 커지게 된다.

표준 정규 분포

평균 0, 표준편차 1인 정규분포 곡선을 말한다.

필요이유

1. 서로 다른 자료를 분석할 수 있다.
2. 확률 계산을 간편하게 할 수 있다.

표준 정규 분포가 없다면 위 정신나간 식 (1)을 계산해야 하는데 표준 정규 분포는 근사값이 미리 계산이 되어있음. 그래서 그냥 갖다 쓰면 됌

중심극한정리

공돌이의 수학정리노트 유튜브 채널 영상

1. 표본 평균의 분포는 정규 분포에 근사하게 된다.
2. 모집단의 모양이 어떻든 관계없다. (모집단이 정규분포가 아니여도 그 모집단의 표본 평균의 분포는 정규 분포에 근사한다.)

이게 왜 중요할까?
우리는 여러 현상을 조사하거나 파악할 때 평균값을 많이 활용하기 때문에 중요하다. 다음의 예시를 살펴보자.

특정 지역에 10000가구가 살고 있다고 하자. 이 지역의 평균 가구 수익을 추정하고자 하는데 전수조사를 하기엔 가구가 너무 많다. 이때 우리는 중심극한정리를 활용할 수 있다. 보편적으로 표본 갯수가 30개 이상일 때, 표본 평균이 정규분포를 띈다고 가정한다. 그래서 우린 30개 가구에 대한 평균값을 확인해서 신뢰도를 나타낼 수 있다. 30개 가구의 평균 가구 수익이 87이라고 하면, 모수의 실제 평균이 87 \(\pm 1 \sigma\) 일 확률이 68% 라고 할 수 있다.