Juneer Blog

이미지 필터링

 
  • Mar 15, 2022

이미지 필터링

Smoothing to Remove Image Noise

이미지의 노이즈를 줄이기 위한 필터가 여러개 존재한다

Box Filter

  • Linear filter
  • 노이즈를 제거하는 가장 간단한 방법 중 하나이며 아이디어는 필터 중간 픽셀값의 이웃 픽셀들의 평균값으로 필터 중간 픽셀값을 대체하는 것이다

  • 3x3 box filter 예시

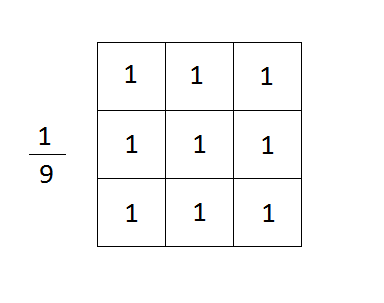
    drawing

  • 코드 구현부

      def getBoxFilter(self, filter_length=3):
    
          # 필터의 모양은 정사각형이라고 간주하며 Normalization을 위해 필터 사이즈의 제곱만큼 스케일링 해줌
          return np.ones((filter_length, filter_length)) / (filter_length**2)

Gaussian Filter

  • Linear filter

  • Gaussian 분포

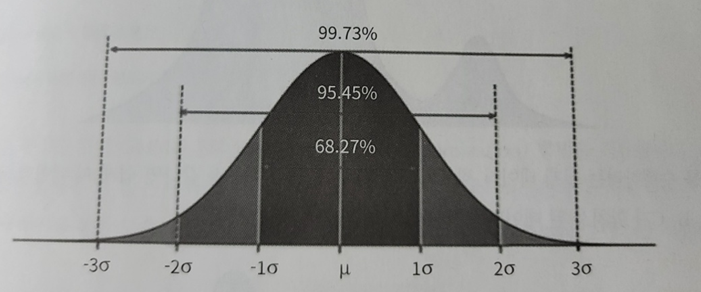
    • 평균 $\mu$와 표준편차 $\sigma^2$에 의해 그 분포가 확정된다. 평균이 0, 표준편차가 1인 정규분포일 경우 표준정규분포라고 한다
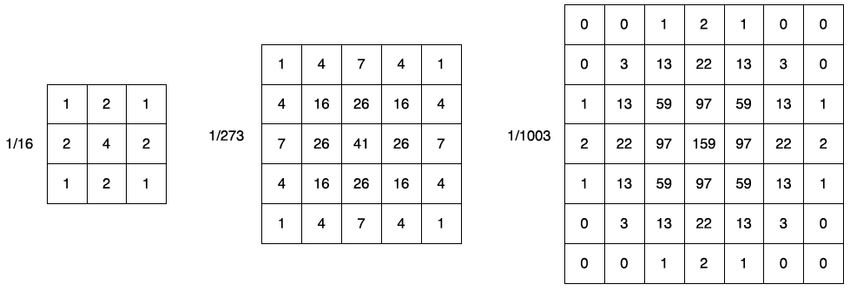
  • Gaussian Filter 수식
\[G(x) = {1 \over {\sigma \sqrt {2 \pi}}} exp^{-x^2 \over 2\sigma ^ 2}\] \[G(x, y) = {1 \over {2 \pi \sigma^2}} exp^{-(x^2 + y ^ 2) \over 2\sigma ^ 2}\]

  • 위 그림의 가우시안 필터에서 볼 수 있듯 가까운 픽셀은 큰 가중치를, 멀리있는 픽셀은 작은 가중치를 사용하여 컨볼루션 연산을 진행함
  • 하지만 위 결과에서 볼 수 있듯 이상치(Noise)가 흐려지기는 하지만 효과적으로 제거하지는 못하며 엣지(Edge)가 blur 처리 되어 상당한 정보손실이 발생한다.

  • 코드 구현부

      def getGaussianFilter(self, filter_length=3, sigma=1):
    
  				# meshgrid를 사용을 위해 지정된 범위의 연속된 배열 선언
          ax = np.linspace(-(filter_length - 1) / 2., (filter_length - 1) / 2., filter_length)
    				
  				# meshgrid를 통한 2차원 평면상의 x, y 좌표 선언
          xx, yy = np.meshgrid(ax, ax)
    
  				# 위 언급한 Gaussian filter 수식 구현
          filter = 1 / (2 * np.pi * np.square(sigma)) * np.exp(-1 * (np.square(xx) + np.square(yy)) / 2 * np.square(sigma))
    
          return filter / np.sum(filter)

Median Filter

  • Nonlinear filter

    • Gaussian filter에 비해 Noise 제거가 좀더 효과적으로 이루어진 것을 확인할 수 있음

    • 그러나 Noise가 salt and pepper 수준이 아니라 위 그림처럼 명확하게 노이즈가 보이지 않을경우 그 효과가 떨어짐

  • 코드 구현부

      def getMedianFilterResult(self, img, palette, index_y, index_x, filter_length=3):
          temp = []       # 필터와 겹치는 이미지의 픽셀값 크기 비교를 위한 일시적 리스트
            
          # 필터 사이즈 만큼 temp리스트에 이미지 픽셀값 추가
          for filter_y in range(filter_length):
              for filter_x in range(filter_length):
                  temp.append(img[index_y + filter_y][index_x + filter_x])
            
          # 리스트의 내부함수인 sort 호출하여 크기순으로 정렬
          temp.sort()
            
          # 정렬된 리스트 값들 중 중간에 위치하는 값으로 palette[index_y][index_x] 대체
          palette[index_y][index_x] = temp[filter_length*filter_length // 2]

Bilateral Filter

  • Nonlinear filter
  • bilateral filter 수식
    • \[g[i, j] = {1 \over W_s} \sum_m \sum_n f[m, n]n_{\sigma_s}[i-m, j-n]n_{\sigma_b}(f[m,n] - f[i,j])\]

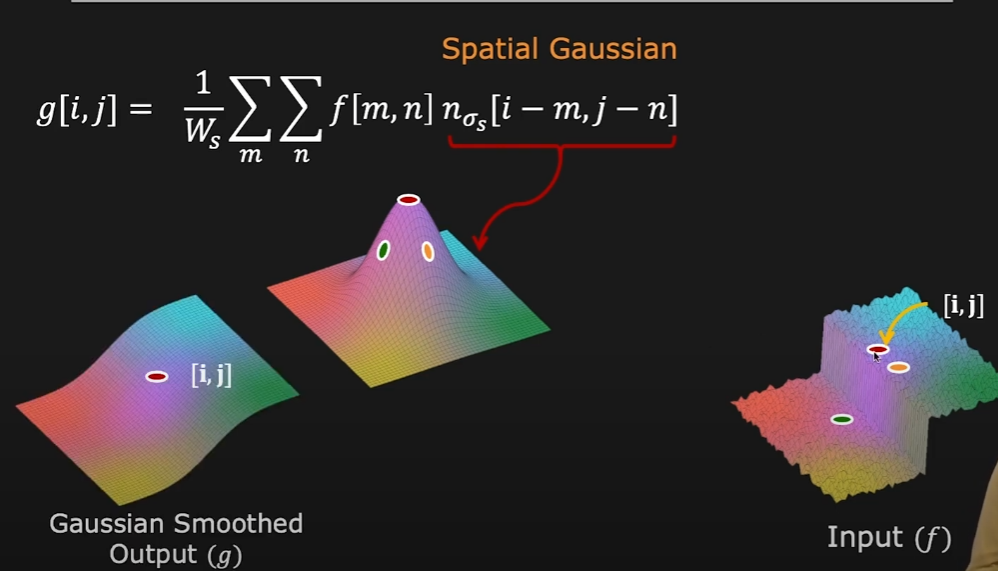
    • 가운데 그림의 Spatial Gaussian filter를 오른쪽 그림 Input에 대해 적용하였을 때 왼쪽 그림과 같은 Gaussian Smootehd Output이 나옴
      • Spatial gaussian filter는 Input이 어떤것이냐에 상관없이 필터 크기에 의해서만 값이 달라지는 필터를 내놓게 됨. 즉 3x3, 5x5, 7x7 필터를 예로 들면 Input이 어떤 것이냐에 상관없이

    • 이번엔 Brightness Gaussian filter를 오른쪽 그림 Input에 대해 적용하였을 때 가운데 그림과 같은 Output이 나옴
      • 위 Brightness Gaussian은 비슷한 Intensity를 지닌 pixel이 있을 경우 높은 weight를 줘서 신호를 살리고 Intensity 차이가 클 경우 낮은 weight를 줘서 신호를 죽임. 예를 들어 Brightness Gaussian 필터(실제로 이런 필터가 있지는 않는것 같지만 잠깐 이렇게 명칭을 쓰자)

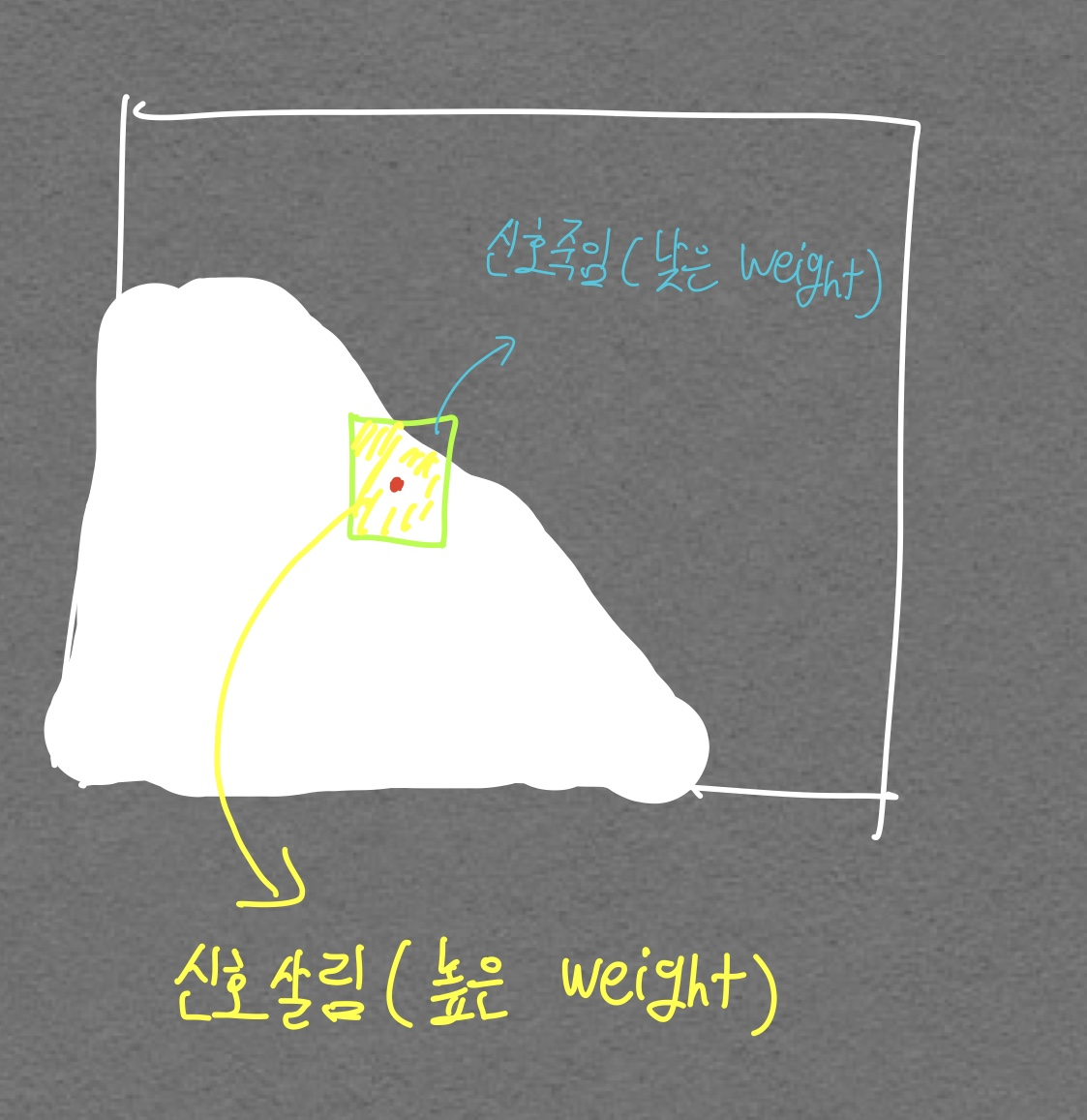
      왼쪽 그림에서 볼 수 있듯 비슷한 Intensity를 가질 경우 높은 weight를 줘서 신호를 살리고 Intensity차이가 클 경우 낮은 weight를 줘서 신호를 죽임. 이를 통해 기존의 Spatial gaussian filter에서 불가능했던 Edge Preserving이 가능함

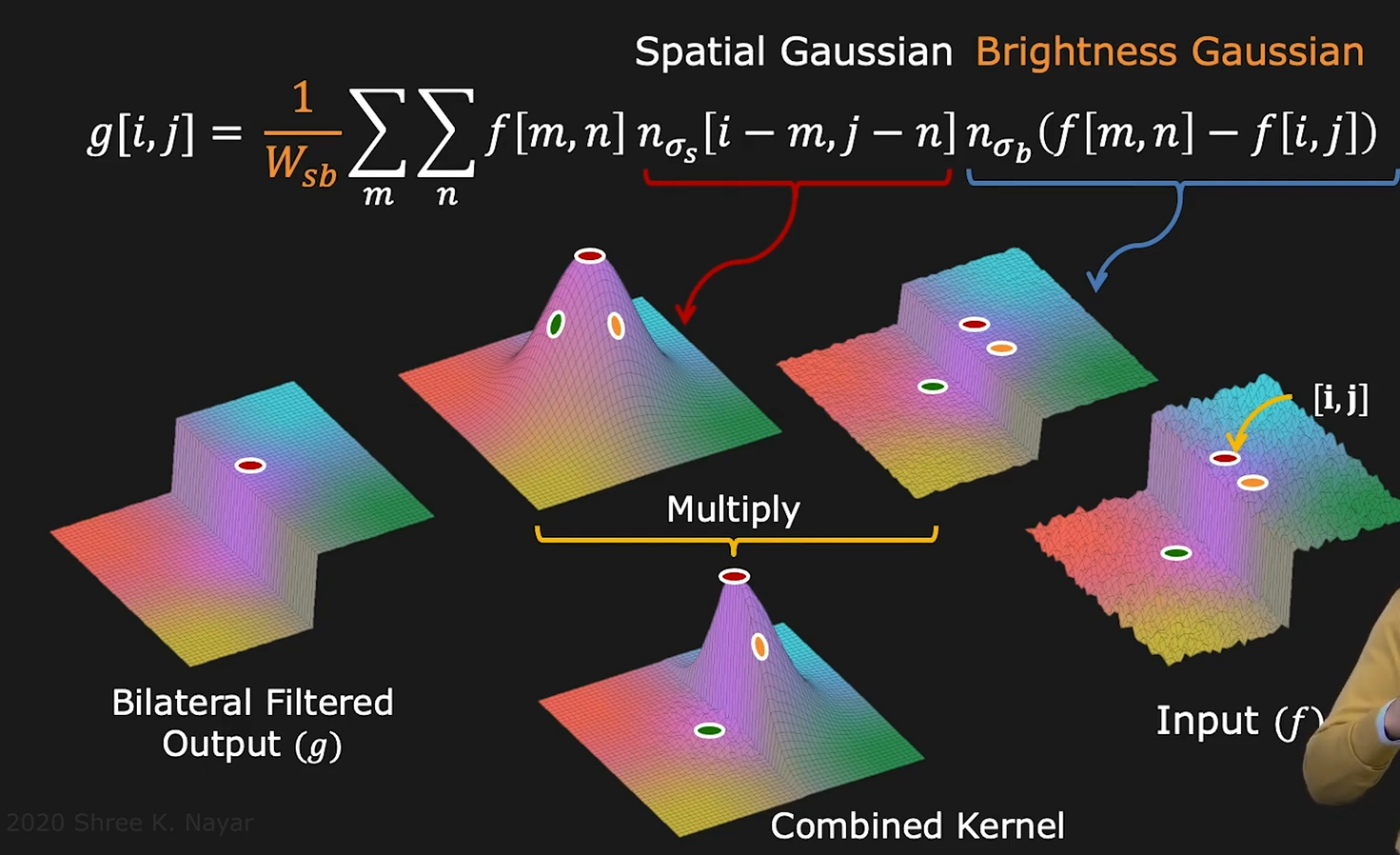
    • 이 두 필터를 곱해서 비슷한 Intensity를 지닌 부분들의 값 분포를 Gaussian 형태로 만들고 엣지와 같이 Intensity 차이가 큰 부분들에는 낮은 weight를 줘서 신호를 없애버리는 Combined 필터를 형성하고 이를 통해 왼쪽 그림의 Bilateral Filtered output을 만들 수 있게 된다
  • 코드 구현부
def getBilateralFilterResult(self, img, palette, index_y, index_x, filter_length=3, sigma_i=20.0, sigma_s=20.0):
        '''
        Convolution 연산을 진행하지 않기 때문에 바로 픽셀값 대체까지 진행함
        '''

        def gaussian(x, sigma):
            return (1.0/(2*np.pi*(sigma**2)))*np.exp(-(x**2)/(2*(sigma**2)))

        def distance(x1,y1,x2,y2):
            return np.sqrt(np.abs((x1-x2)**2-(y1-y2)**2))
        
        wp_total = 0
        filtered_image = 0
        for k in range(filter_length):
            for l in range(filter_length):
                n_x = index_y - (filter_length/2 - k)
                n_y = index_x - (filter_length/2 - l)

                if n_x >= len(palette):       # index error 방지. 이미지 범위 초과시에도 반대쪽 픽셀을 가리킬 수 있도록 함
                    n_x -= len(palette)
                if n_y >= len(palette[0]):
                    n_y -= len(palette[0])
								
								# Brightness Gaussian 구하는 부분
                gi = gaussian(img[int(n_x)][int(n_y)] - img[index_y][index_x], sigma_i)

								# Spatial Gaussian 구하는 부분
                gs = gaussian(distance(n_x, n_y, index_y, index_x), sigma_s)
                wp = gi * gs
                filtered_image = (filtered_image) + (img[int(n_x)][int(n_y)] * wp)
                wp_total = wp_total + wp
        filtered_image = filtered_image // wp_total
        palette[index_y][index_x] = int(np.round(filtered_image))

# 위 코드는 아래 깃허브 소스코드를 참고함
# https://github.com/anlcnydn/bilateral

이미지 적용 결과

3x3 크기 필터 적용

  • gray.png

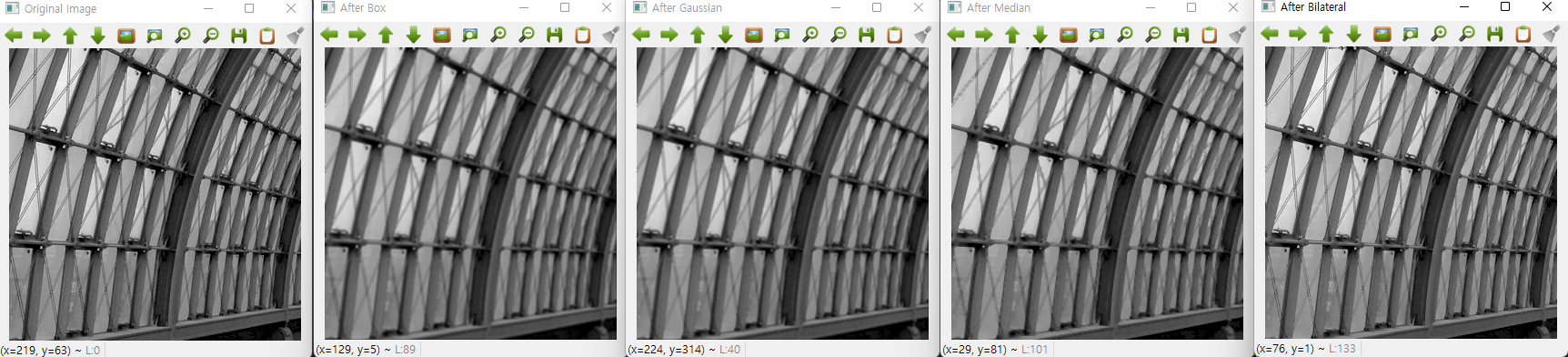
  • gray_n1.png

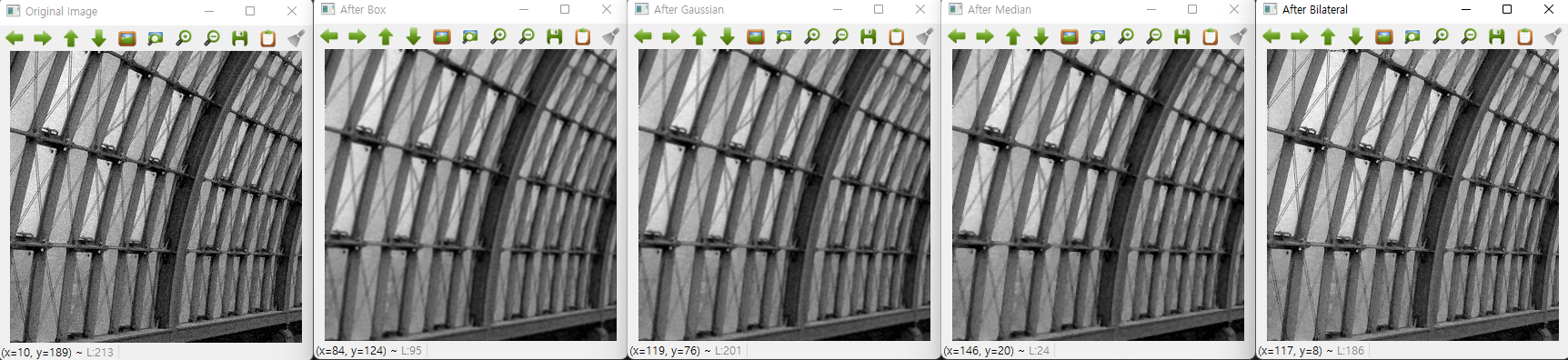
  • gray_n2.png

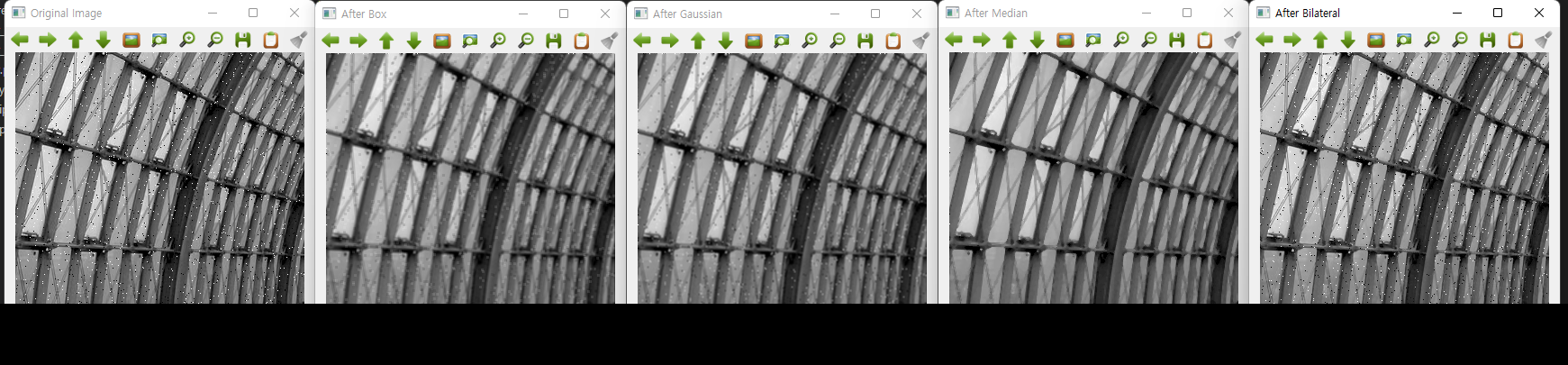
5x5 크기 필터 적용

  • gray.png

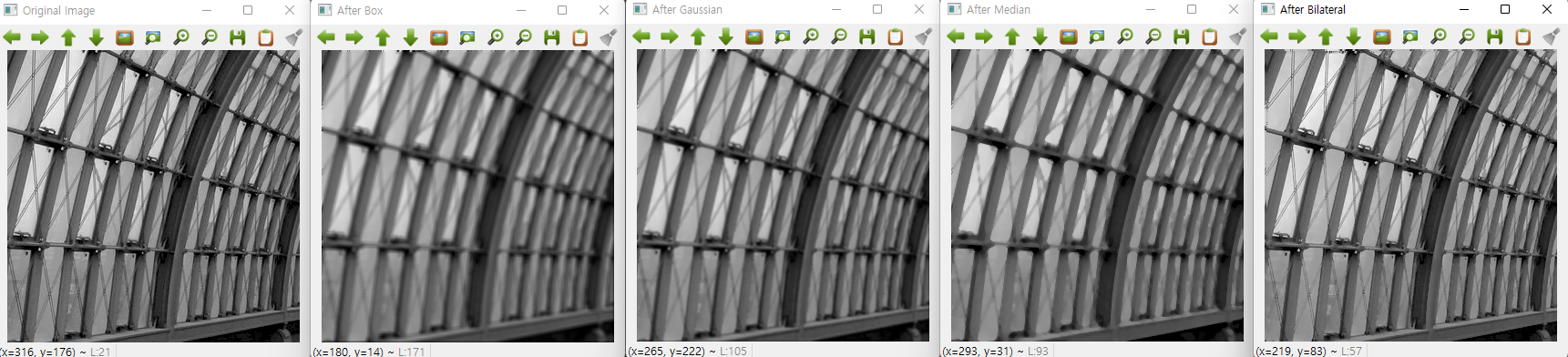
  • gray_n1.png

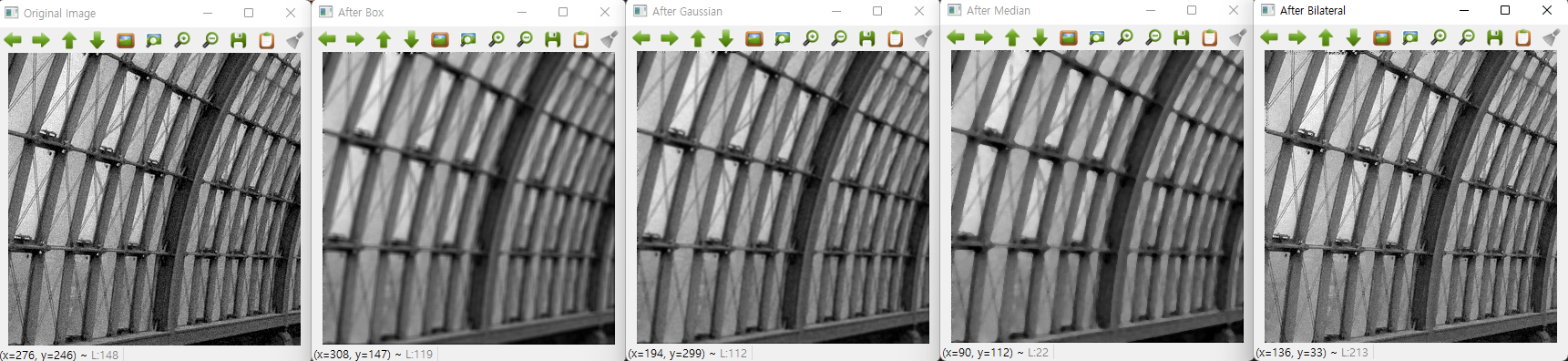
  • gray_n2.png

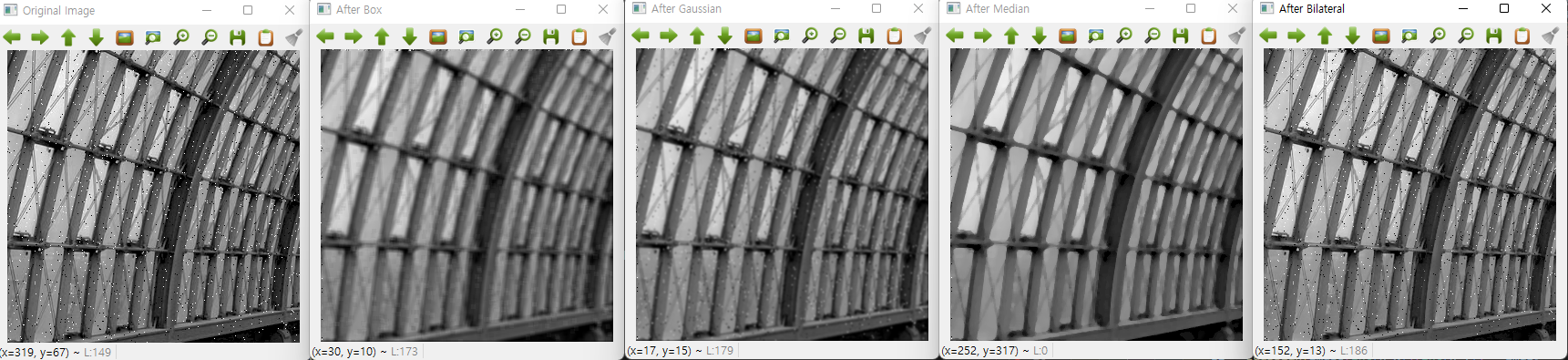
출처

Search