Kernel Density Estimation

밀도추정(Density Estimation)

파이썬 머신러닝 완벽가이드 책을 읽다가 KDE(Kernel Density Estimation)에 대한 개념이 나와서 작성함

우리가 확인할 수 있는 데이터는 어떤 변수가 가질 수 있는 다양한 가능성 중 하나가 구체화 된 것
데이터의 본질, 특성을 파악하기 위해서는 하나로는 부족. 많은 수의 데이터를 봐야함
- 많은 수의 데이터를 봄으로써 데이터의 분포를 확인할 수 있고 이 분포로부터 원래 변수의 확률 분포 특성을 추정하는것이 밀도추정

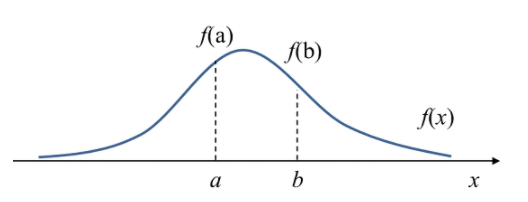
위 그림에서 $f(a)$는 $x = a$에서 확률밀도(Probability density) 즉, 변수 $x$가 $a$라는 값을 가질 상대적인 가능성(relative likelihood)
- 용어 헷갈리지 않기
  - 밀도(Density): $f(a)$와 같이 확률밀도함수의 확률값
  - 확률(Probability): 주어진 구간에서의 확률밀도함수의 적분값(면적) $P(a \leq x \leq b) = \int^a_b f(x)dx$
밀도추정의 방법은 2가지
1. Parametric
  - 모델을 정해놓고 데이터로부터 모델의 파라미터만 추정하는 방식
    - 예로 일일 교통량이 정규분포를 따른다고 가정한다면 관측된 데이터들로부터 평균과 분산만 구하면 되기 때문에 밀도 추정 문제가 간단해져버림
      - 뒤에 커널함수 얘기 나오는데 커널함수도 결국 함수 하나를 지정하는 순간 위 사례처럼 특정 분포를 가정해버리는것이니 Parametric 문제 아닌가..? 아직 잘 모르겠다..
2. Non-parametric
  - 대표적 방법은 히스토그램(Historgram)
    - 히스토그램은 각 데이터구간의 경계면(bin)에서 불연속성이 나타나는 것과 bin의 크기 및 위치에 따라 히스토그램이 달라진다는 것, 고차원 데이터에 메모리 등으로 사용하기 힘들다는 문제가 있음
    - 위 단점을 해결하기 위한것이 KDE(커널 밀도 추정 - Kernel density estimation)

커널함수를 이용해 확률 밀도 함수를 추정하는 방법
커널함수란
1. 원점을 중심으로 대칭
2. 적분값이 1인 음이 아닌 함수
  - 수식으로 표현하면 $\int^\infty_{-\infty} K(u)du = 1 \\ K(u) = K(-u), K(u) \geq0, \forall u$
  - 대표적인 커널함수로 가우시안, Epanechnikov, uniform 함수등이 존재
커널함수가 확률밀도함수를 추정하는 식

$\hat{f}_h(x) = {1 \over n} \sum^n_i K_h(X - x_i)$ h는 커널이 뾰족한 형태(h가 작은 값)거나 커널이 완만한(h가 큰 값)인지 조절하는 파라미터

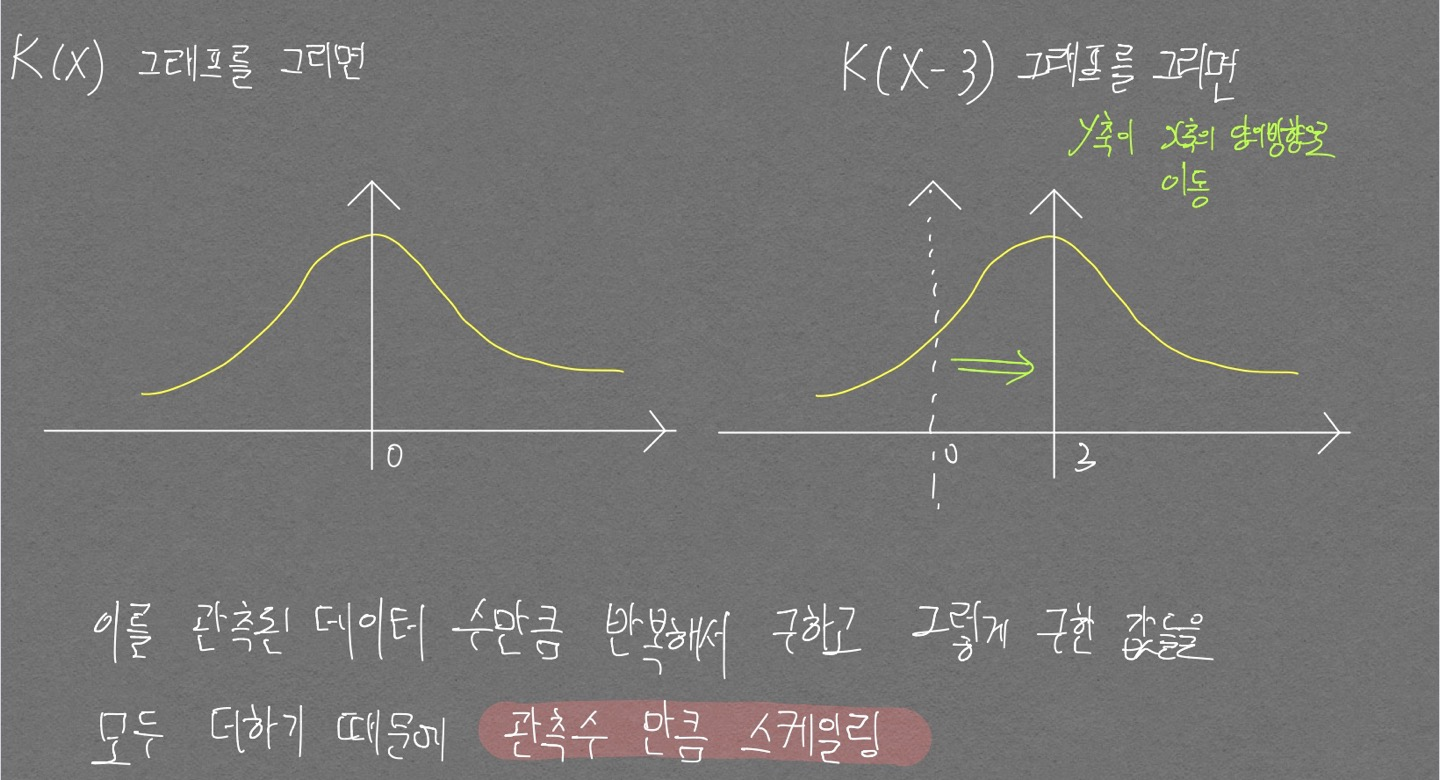
KDE 결과 예시

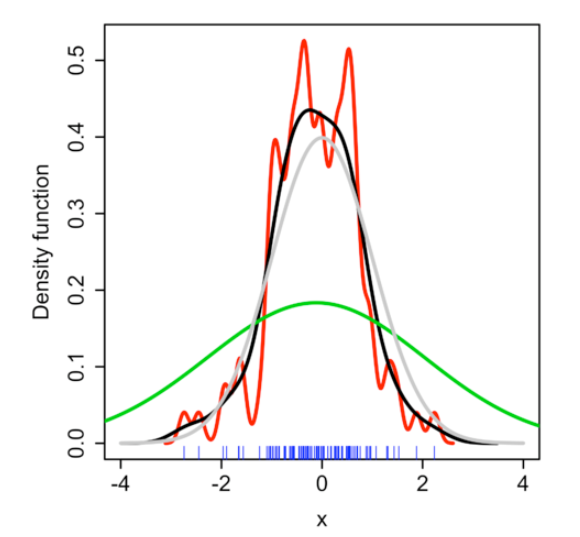
어떤 커널함수를 사용하는가, 파라미터 h 값(Bandwidth 라고도 부름)을 어떻게 하느냐에 따라 결과는 달라질 수 있다
가우시안 커널함수를 사용할 경우 최적의 h 값은 아래와 같다고 한다

$h = ({4\sigma^5 \over 3n})^{1 \over 5} \approx 1.06\sigma n^{-1 \over 5}$

PREVIOUS경제