선형변환 (Linear Transform)

• Feature Vector를 하나의 공간에서 다른 공간으로 투영하는 것

분산

• 한 변수의 데이터 변동

공분산

• 두 변수가 함께 변경되는 정도
• $cov(X, Y) > 0$ 면 X가 증가할 때 Y도 증가함

공분산 행렬

• 여러 변수와 관련된 공분산을 포함하는 정방 행렬(Square Matrix)이며 대칭 행렬(Symmetric Matrix)
  • 대칭행렬 $A^T = A$
    • 대칭행렬은 고유값 분해(Eigen Decomposition)와 관련한 매우 좋은 특성을 가짐
      • 고유벡터를 직교행렬로 만들 수 있다 (아직 이해는 안감)
      • 고유값을 정방 행렬로 대각화 할 수 있다

고유벡터(Eigen Vector), 고유값(Eigen Value)

• 행렬 A를 곱해도(선형변환해도) 방향은 변하지 않으며 크기만 변하는 벡터. $Ax = \lambda x$ 인 $x$. ($x \neq 0$)
  • 좀더 말로 쉽게 풀면 선형변환 A에 의한 변환 결과가 자기 자신의 상수배가 되는 0이 아닌 벡터. 이 상수배 값을 고유값(Eigen value)라 함

  • 아래 그림에서 빨간 벡터는 고유벡터 x, 파란벡터, 분홍벡터가 고유벡터이며 이때 파란벡터는 특정 상수배만큼 커짐. 이때의 상수배가 고유값

    

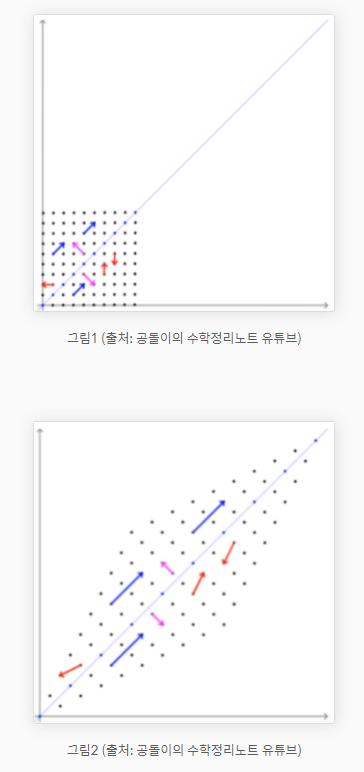
• 위 식의 정의를 통해 유도할 수 있는 것
  • $Ax - \lambda x = 0
    (A- \lambda I)x = 0$ 이며 $x$가 영벡터가 아니므로 $(A - \lambda I)$는 역행렬이 없어야 한다. 즉 det $(A - \lambda I)$
    • 위 행렬식을 통해 고유값과 고유벡터를 찾을 수 있음
• 여러개 존재할 수 있음
• 고유벡터, 고유값은 정방행렬에 대해서만 정의됨
  • A는 반드시 정방행렬A가 정방행렬이라면 최대 그 차원의 수 만큼 고유벡터를 가질 수 있음 2x2 행렬은 2개, 3x3 행렬은 3개

고유값 분해(Eigen Decomposition)

• 고유벡터, 고유값을 이용해 행렬을 분해할 수 있다. 공분산 행렬을 C라고 하면 \(C = P \sum P^T \\ C = \begin{bmatrix}e_1 \cdots e_2\end{bmatrix} \begin{bmatrix}\lambda_1 &\cdots &\lambda_2 \\ \cdots & \cdots &\cdots \\ 0 & \cdots & \lambda_n \end{bmatrix}\begin{bmatrix}e^t_1 \\ \cdots \\ e^t_n\end{bmatrix}\)
  • 위에서 P는 n x n 직교행렬, $\sum$은 n x n 정방행렬, $e_1$은 가장 분산이 큰 방향을 가진 고유벡터, $e_2$는 $e_1$에 수직이면서 다음으로 가장 분산이 큰 방향을 가진 고유벡터