나를 7년동안 괴롭혔던 선형(Linear)라는 단어를 이 포스트를 통해 처단하고자 한다…

선형대수학을 배우는 이유

• 어떤 대상 사이의 상호작용을 해석하는 능력을 기르기 위함

 

(중요) 행렬과 벡터, 그리고 선형변환을 어떻게 바라보면 되겠는가?

\[AX = b\]

위 식에서 행렬 \(A\) 의 열벡터는 다음을 반드시 명심해야 한다.

• 하나의 열벡터는 공간상에서 하나의 화살표를 의미한다. (시각화가 불가능한 고차원에서도 똑같이 적용되는 것임)

\(X\) 는 다음을 반드시 명심해야 한다.

• X 벡터(열벡터 하나이므로 벡터라고 명해도 된다)는 이미 완성되어 있는 화살표들의 길이를 스케일링 해주는 역할을 한다

  

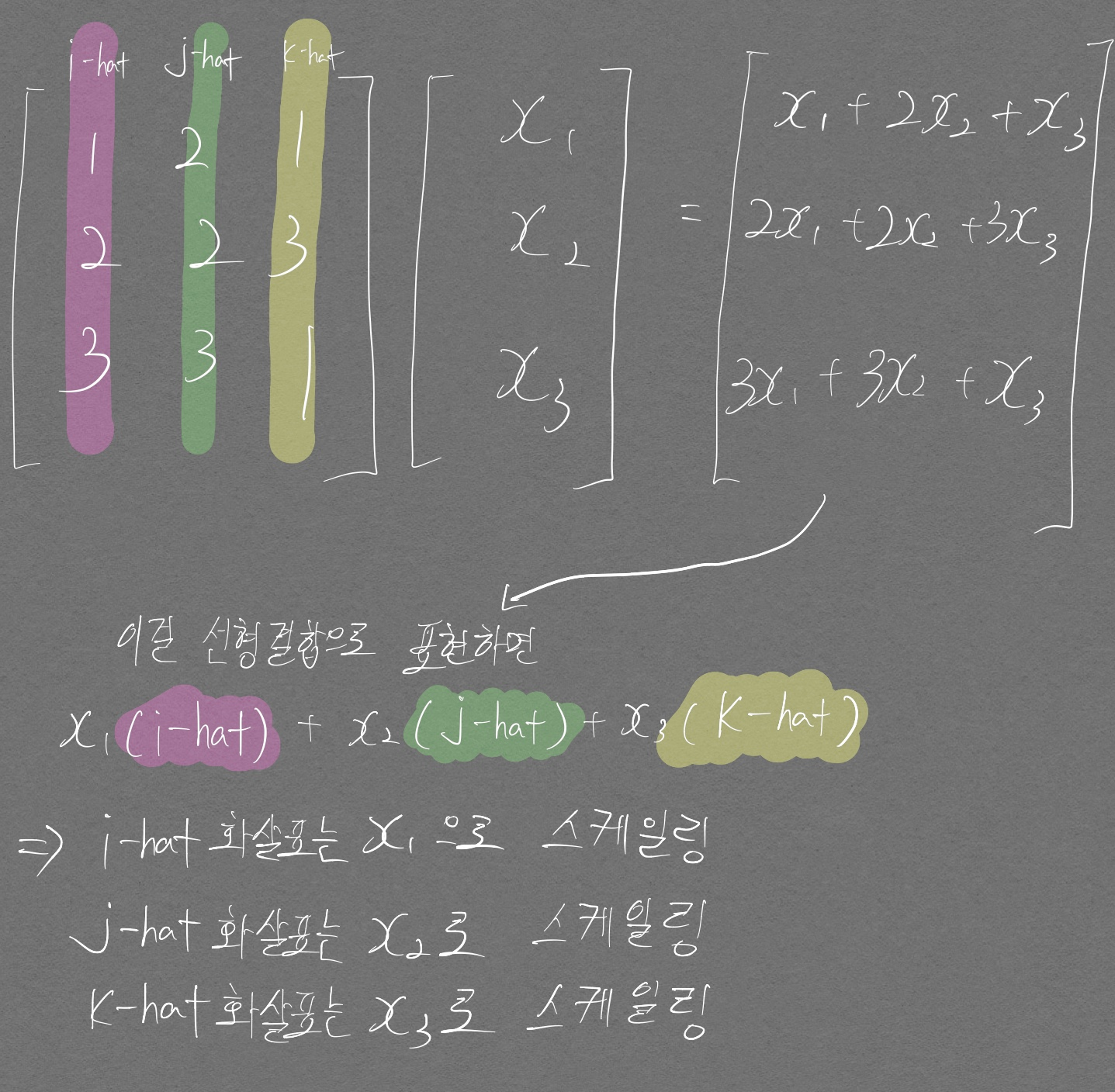
  • 위와 같이 스케일링이 끝난 화살표들이 합쳐진것이 \(b\) 이다.

그리고 선형변환은 공간을 이동시키는 방법이다.

• 공간을 이루는 기저 벡터¹를 변형시켜도
  1. 그 공간을 구성하는 수많은 격자선들은 여전히 모두 평행하며 균등간격을 유지한다.
  2. 원점은 그대로다.

선형(Linear)이란

아래 식은 선형대수학을 공부한 사람이라면 상당히 자주 봤을 수식이다.

\[f(x_1 + x_2) + f(x_2) = f(x_1) + f(x_2)\] \[f(kx) = kf(x)\]

위 수식을 만족하는 함수 f(x)를 선형(Linear)라고 한다. 내가 계속 궁금했던 것은 그 똑똑한 과거의 수학자들이 많고 많은 식 중 왜 저러한 성질을 가지는 것을 선형이라고 칭했냐는 것이다.
계속 공부해봐야 겠지만 스스로한테 여태까지 가장 납득이 되는 설명을 찾았으며 이는 선형결합을 알아야 한다.

선형결합(Linear combination)

집합 A의 원소 \(x_1, x_2, ... , x_n\)과 상수 \(a_1, a_2, ... , a_n\)을 곱하여 더한 \(a_1x_1 + a_2x_2 + ... + a_nx_n\) 결과값(즉, 스칼라)을 선형결합이라고 하며 이 선형결합 값이 집합 A에 속하는 경우 이를 선형이라고 한다.

이를 더 이해하기 쉽게 식으로 예를 들어 설명해보면

\(f(x) = 2x + 3\) 이라는 함수가 있을 때 이 함수는 선형이 아니다. 왜냐하면 \(f(x_1+x_2) \neq f(x_1) + f(x_2)\) 이고 이것을 그림으로 표현해보면 아래와 같기 때문이다.

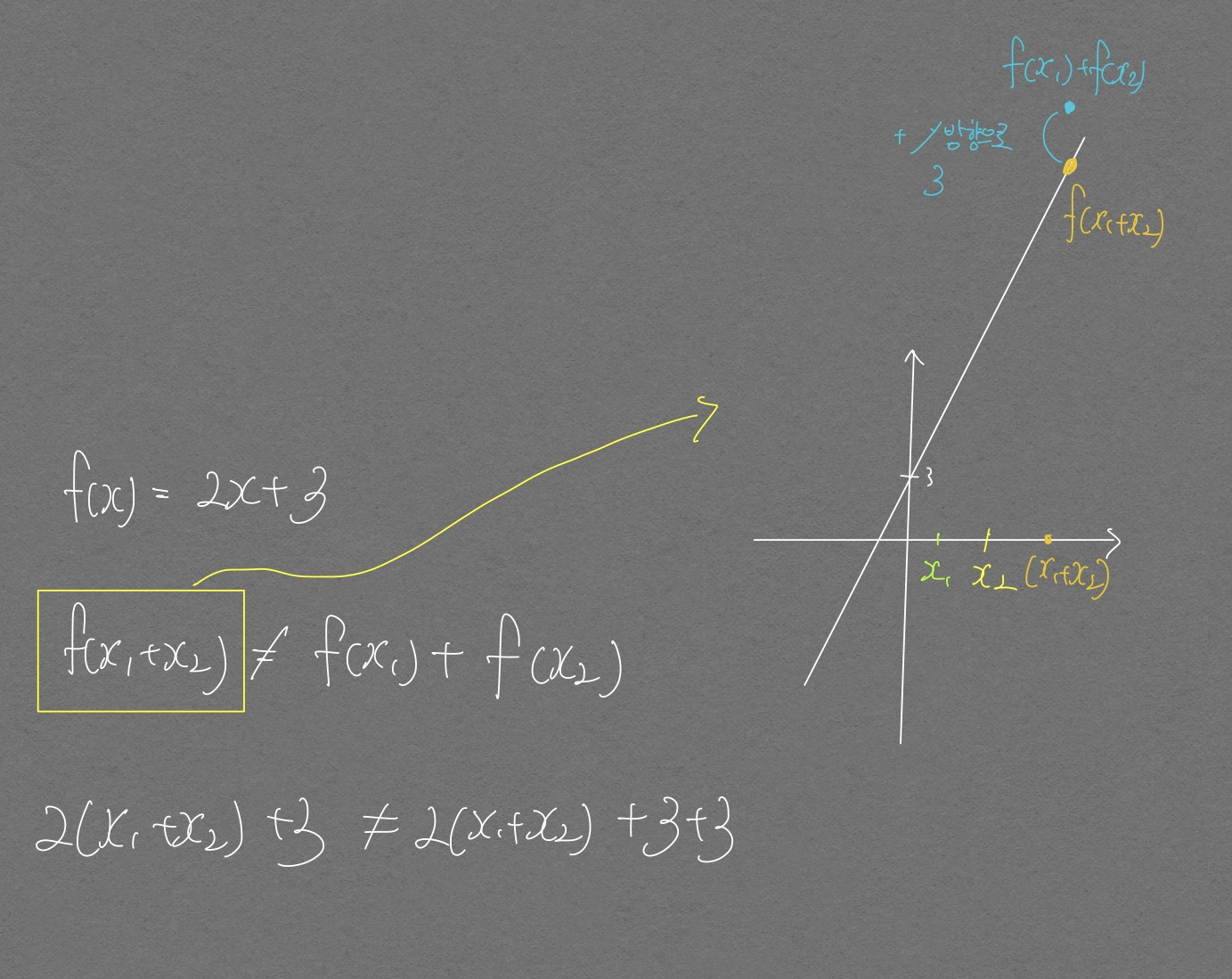
위 그림이 시사하는 바는 다음과 같다.

• \(f(x_1 + x_2)\) 의 값은 \(f(x)\) 위에 존재한다. 즉 위 선형결합 부분에서 언급한 집합 A에 속하는 경우라는 말을 여기에 대응시켜 볼 수 있다. 선형 시스템이 예측 가능하다고 여러 글에서 본 적이 있는데 예측 가능한 이유가 바로 이러한 점 때문으로 보인다.
  • 위 그림을 보고 \(f(x_1) + f(x_2) = f(x_1 + x_2) + 3\) 이라는 관계식을 세우면 역시나 예측 가능해지는 것이지 않은가라는 생각이 들기는 하지만 집합 A에 속하지 않는다는 점이 수학세계에서 상당히 강력한 역할을 하기에 이런 선형이라는 개념이 생기지 않았나 싶다.
• \(f(x) = 2x + 3\) 은 원점을 지나지 않기 때문에 선형이 아니다.

선형 방정식(Linear Equation)

일차 방정식 이라고도 한다. (일차 방정식은 되게 쉬운 느낌인데 선형 방정식이라고 하니까 거부감이 드는건 기분탓..?)

\[a_1x_1 + a_2x_2 + ... + a_nx_n = b\]

위 식과 같은 꼴이면 선형 방정식이라고 부르며 방정식 개념이 모호하다면 방정식 포스트를 확인하자

선형 시스템(Linear System)

선형 방정식이 여러개로 이루어져 있다면 그것이 곧 선형 시스템이다.
일반적으로 선형시스템은 n개의 변수를 가진 m개의 선형방정식으로 이루어지며 형태는 아래 식과 같다.

\[a_{11}x_1 + a_{12}x_2 + ... + a_{1n}x_n = b_1 \\ a_{21}x_1 + a_{22}x_2 + ... + a_{2n}x_n = b_2 \\ \vdots \\ a_{m1}x_1 + a_{m2}x_2 + ... + a_{mn}x_n = b_m\]

\(b_1 = b_2 = ... = b_m = 0\) 일 경우 위 식을 homogeneous system 이라고 한다.

여기서 homogeneous(동차)의 단어 의미? 동차함수 예를 통해 그 의미를 어느정도 이해해 볼 수 있다.
\(f(ax) = a^kf(x)\)
위 방정식은 동차함수로, 독립변수를 a배 증가시켰을 때 함수값이 \(a^k\)배 증가하는 함수를 말한다. 즉 a의 거듭제곱 배 만큼 증가하는 함수를 말한다. k는 어느값도 될 수 있으며 위 함수를 k차 동차함수 라고 한다.

homogeneous system 에서 \(x_1 = x_2 = ... = x_n = 0\) 은 항상 해가 되며 이를 trivial solution 이라고 한다.
\(x_1, x_2, ... , x_n\) 중 어느 하나라도 0이 아닌 경우의 해를 nontrivial solution 이라고 한다.
선형 방정식들이 같은 해를 가질 경우 두 방정식을 동치(Equivalent) 관계에 있다고 한다.

선형 독립(Linear Independence)

강의 노트에서 lambda가 solution으로 표기해놨음. 헷갈리지 말자. 여기 설명에서는 x가 solution이 아니라 lambda가 solution임.

\(v = \lambda_1x_1 + ... + \lambda_kx_k\) 인 선형 결합(Linear combination)이 있을 때 trivial solution일 경우에만 \(\sum^{k}_{i=1}\lambda_ix_i = 0\) 이라고 하면 \(x_1, x_2, ... , x_k\) 를 포함하는 집합 \(X\) 는 선형 독립(Linear Independence)이다.

Norm

Norm은 한 벡터의 크기를 의미한다.

• Vector space를 실수(R)로 보내는 함수이며 3가지 성질을 가짐
  1. Absolutely homogeneous: \(\lVert \lambda x \rVert\ = \vert\lambda \lVert x \rVert\)
     • 실수의 Norm 은 그저 절대값만 취해주면 됨
       • why? 실수의 Norm은 1차원으로 굉장히 자주 쓰여서 |를 하나씩만 두는것으로 일종의 약속을 함
  2. Triangle inequality: \(\lVert x + y \rVert \leq \lVert x \rVert + \lVert y \rVert\)
  3. Positive definite: \(\lVert x \rVert \geq 0 and \lVert x \rVert = 0 \Leftrightarrow x = 0\)

• General formula

  \[\vert\vert W \vert\vert_p = (\sum_{i=1}^n \vert W_i \vert ^p)^{1 \over p}\]
  • i는 \(W\)를 이루는 element 개수
  • p는 사용자가 지정할 수 있는 Hyper parameter
• $L_2$ norm 예시

\[\vert \vert W \vert\vert_2 = \sqrt{W_1^2 + W_2^2} = \sqrt{W^TW}\]

벡터 공간(Vector Space)

벡터를 다룰 수 있는 공간을 의미하며, 우리가 이 공간을 자유자재로 사용하기 위해선 2가지를 알아야 한다.
3blue 1brown 의 선형대수학 편에서 자주 볼 수 있는 부분인데, 2차원 공간에서 내가 원하는 곳에 화살표를 갖다 놓으려면

1. 벡터와 벡터간의 합을 할 수 있어야 한다.
2. 하나의 벡터에 대해서 스칼라와의 곱을 통한 스케일링을 할 수 있어야 한다.

이걸 똑똑한 사람들이 있어보이게 표현한 말이 벡터공간에서 합연산과 곱연산을 정의해야한다 라는 것이다. 참 말 이해하기 어렵다.. ㅋㅋ;

\[V_1 + V_2, KV_2\]

합연산과 곱연산은 아직 정하지 않았으며(우리가 상식으로 알고있는 합과 곱이 아닐수도 있다. 사용자가 정의하기 마음이다.) 합연산과 곱연산을 정한뒤에 다음의 성질들을 만족하는지 점검해야 한다

• 합연산에 대하여
  1. 닫혀있는가? \(\forall V_1, V_2 \in V_n, V_1 + V_2 \in V_n\)
  2. 교환법칙 성립하는가? \(\forall V_1, V_2 \in V_n, V_1 + V_2 = V_2 + V_1\)
  3. 결합법칙 성립하는가? \(\forall V_1, V_2, V_3 \in V_n, (V_1 + V_2) + V_3 = V_1 + (V_2 + V_3)\)
  4. 항등원이 존재하는가? \(\forall V_1 \in V_n, \exists e \in V_n \quad s.t. V_1 + e = V_1\)
     • 여기서 s.t.는 such that(뒤에 말 강조하는 느낌..! 그냥 that 이라고 말해도 될꺼 such 까지 써서)
     • 또한 이때 e는 \(\vec{0}\), 즉 영벡터이다.
  5. 역원이 존재하는가? \(\forall V_1, \in V_n, \exists x \in V_n \quad s.t. V_1 + x = 0\)
• 곱연산에 대하여
  1. 닫혀있는가? \(\forall K \in R, \forall V \in V_n, KV \in V_n\)
  2. 결합법칙 성립하는가? \(K_1, K_2 \in R, \forall V \in V_n, K_1(K_2V) = (K_1K_2)V\)
  3. 항등원이 존재하는가? 실수곱셉의 항등원 1에 대해 \(\forall V \in V_n\) 은 \(1 \cdot V = V\) 를 만족한다
     • 역원은 스칼라 1이 결과값이므로 다루지 않는다. 우린 결과값이 벡터가 되는걸 원하는건데 스칼라가 나오니까 안구함
  4. 분배법칙이 존재하는가? \(\forall K_1, K_2 \in R, \forall V_1, V_2 \in V_n \\ (K_1 + K_2) \cdot (V_1 + V_2) = K_1V_1 + K_2V_1 + K_1V_2 + K_2V_2\)
     • 합연산, 곱연산 두가지를 정의했으므로 이 두가지 사이의 법칙인 분배법칙이 성립하는지 검사하는것

이 검사들이 끝나고 모두 통과한다면 드디어 \(V_n\)은 벡터 공간이라고 할 수 있는것!
이 말을 다시 한다면, 위 9가지 법칙만 통과하면 벡터라고 생각해도 무방하다는 것.
이 말이 나중에 수학 빡고수가 되었을 때 요긴하게 쓰일 수 있을 말로 보인다.

부분 공간(sub space)

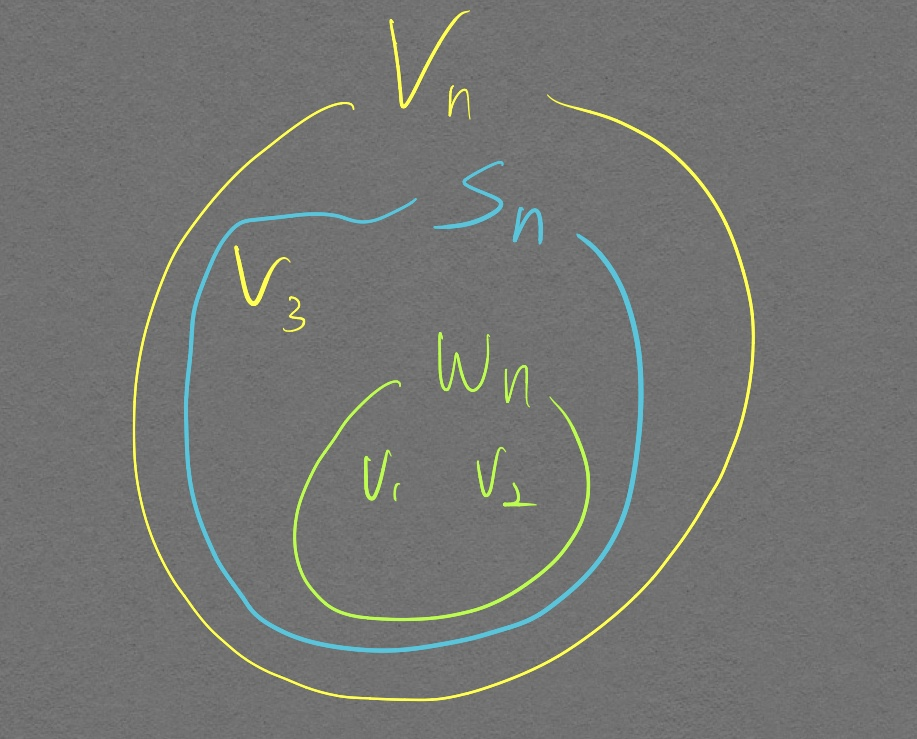
$ W_n $ 집합에서 두 벡터의 합 연산을 통해서 $ V_3 $ 를 표현할 수 없다. 그러나 $ S_n $ 은 $ V_n $ 을 만들기 위한 벡터(화살표)를 모두 가지고 있기 때문에 벡터 $V_n$ 의 부분 공간이다.

어떤 벡터 공간의 부분 집합이 부분 공간인지 알기 위해서는 합연산, 곱연산에 대해 닫혀있는지만 파악하면 된다.
나머지 모든 속성들은 이미 어떤 벡터 공간에 속하는 벡터(화살표)들 이라는 점에서 만족되었기 때문에 닫혀있는지만 파악하면 된다.

Affine space

이해가 가장 잘되는 Affine 변환 설명 블로그 Affine 변환 설명 블로그: 시간날 때 이 블로그 설명을 좀더 심도있게 읽으면 좋을것으로 생각된다.

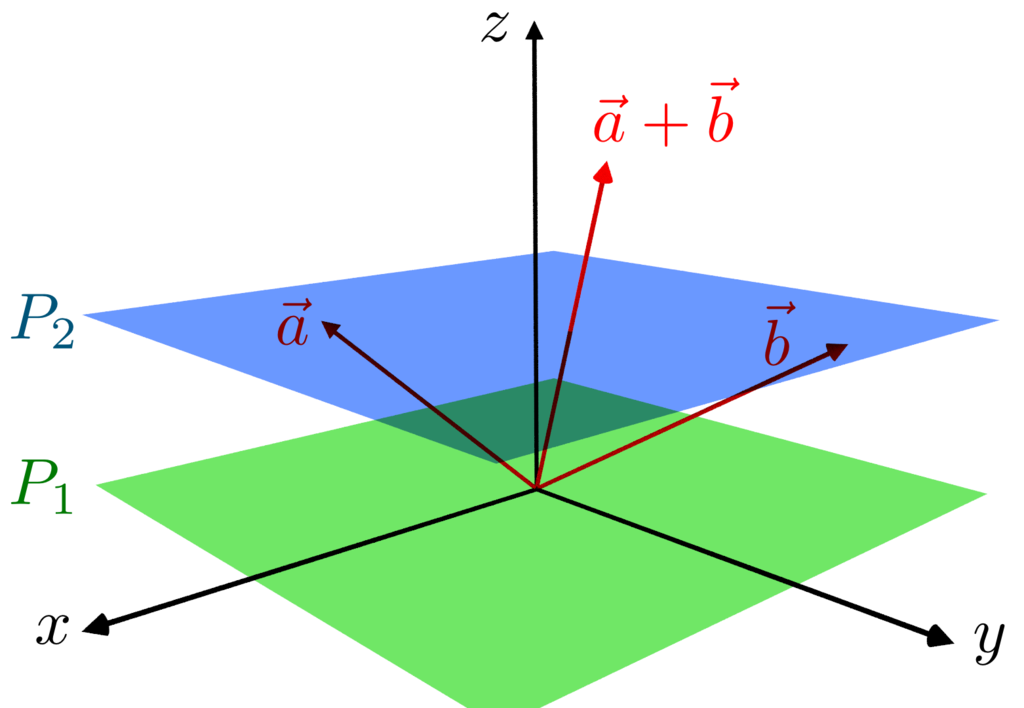
• 벡터공간은 아니지만 벡터공간의 속성을 유용하게 사용할 수 있는 경우가 많다.
  • 원점을 지나지 않기 때문에 벡터 공간이 아님

기저(Basis)

벡터 공간 \(V\)가 있다고 가정할 때 이 \(V\)의 부분 공간 \(S\)가

1. 선형독립이며
2. S가 span되면 V가 된다고 할 때(즉, V 벡터 공간을 형성하기 위한 화살표들이 준비가 되어있다면)
   • 이때 span은 준비되어있는 화살표 스케일링해서과 합 연산을 통해 표현할 수 있는거 싹 다 표현하는것을 의미함.

이 S를 기저(Basis)라고 한다.

이 basis는 유니크한가?
그렇지 않다. 하나의 벡터 공간에 대해 수많은 basis가 존재할 수 있다.

한 벡터에 대한 선형 변환이 어떻게 작동되는지를 알고싶다면, 선형 변환 이후 기존의 기저 벡터가 어떻게 변하는지를 알면 된다.

랭크(Rank)

임의의 행렬 A가 있을 때 이 행렬의 Rank는 이 행렬의 열벡터로 생성할 수 있는 벡터 공간의 차원을 의미한다.
여기서 중요한 사실이 하나 있는데, 행벡터의 Rank와 열벡터의 Rank는 항상 동일하다는 것이다.

풀 랭크(Full Rank)

임의의 행렬 \(A \in R^{m \times n}\)가 가질 수 있는 최대로 가능한 Rank 값.
행과 열의 각각의 Rank는 서로 같은 값을 가진다고 하였으므로, Rank(A) = Min(m,n)

내적(Inner product)

• 굉장히 큰 도움이 된 영상

예전부터 많이 듣던 용어들.. Inner product, Dot product, cross product, outer product… 그 개념을 확실히 잡자
Inner product는 Dot product를 포함하는 일반적 개념 이다.

이해를 위해 반드시 선행되어야 하는것이 바로 고정관념 부수기이며, 나는 개인적으로 다음 2개의 고정관념을 탈피하는것이 큰 도움이 된다고 생각한다.

필요 조건

1. 합, 곱과 같은 연산은 사용자가 정의한 것이며, 새로운 연산을 직접 정의할 수도 있다.
2. 숫자는 크기를 나타내고, 문자는 크기라는 개념이 없어서 두 체계(숫자, 문자간의)에는 차이가 있어 보이지만, 숫자와 문자가 같은 연산을 사용하고, 숫자 하나하나를 문자 하나하나로 매핑할 수 있다면 결국 숫자도 정해진 연산 체계 안에서 움직이고 있는 원소일 뿐이다. 그래서 수학적 일반화를 문자를 통해서 진행해도 이를 숫자에 대응시키는건 너무나도 자연스러운 것이다. (동형 사상에 의해)

지금부터 벡터공간에서의 내적을 정의할 것이며 그 흐름을 그냥 받아들여 보자.

• 벡터공간임을 강조한 이유는 벡터 공간이 아닌 다른 공간이여도 내적 정의가 가능하다는 의미라는 것
• 벡터공간에서 벡터끼리 합치는 연산, 벡터와 상수로 스케일링 하는 연산이 이미 정의가 되어있어서 사용 가능하다는 것
  • 이 연산들도 벡터 공간이 아닌 다른 공간이라면 그 공간만의 연산이 존재할 것이고, 그 특수한 연산에 의한 내적이 정의될 수 있다.

어떤 집합에서 원소 2개 u, v가 있다고 하자. 이때 u 내적 v, 즉 \(u \cdot v\)를 정의해보자

1. 교환법칙 성립해야 한다. \(u \cdot v = v \cdot u\)
2. 분배법칙 성립해야 한다. \((u + v) \cdot w = u \cdot w + v \cdot w\)
3. 동차성을 만족해야 한다. \((ku) \cdot v = k(u \cdot v)\)
4. 자기 자신과 내적하면 값이 무조건 0 혹은 양수여야 한다. 또한 내적 결과가 0 벡터가 나올시 연산에 사용된 벡터는 반드시 0 벡터이다. (이 속성을 만족하는 행렬은 Positive definite로 불린다)

\[v \cdot v \geq \overrightarrow{0}\] \[v \cdot v = 0 \Leftrightarrow v = \overrightarrow{0}\]

내적 연산의 Norm

이제 이 내적이 어떻게 벡터 공간에서 활용될 수 있는지 살펴보자.
벡터 공간에서 중요하게 여기는 것중 하나는 Norm을 통한 크기 비교이다.

그리고 이 크기 비교에 사용되는 유명한 수학자의 식이 바로 코시-슈바르츠 부등식이다.

\[\lvert \langle u, v \rangle \rvert^2 \leq \langle u, u \rangle \cdot \langle v, v \rangle\]

이 코시-슈바르츠 부등식은 굉장히 여러 분야에서 사용되는 부등식이다. 난 이 부등식을 다음과 같이 여기니 어느정도 받아들여졌다.
코시-슈바르츠 부등식은 두 원소에 대해 정의한 연산을 진행한 것의 크기는, 각각의 원소의 크기에 대해 연산을 진행한것보다 항상 작거나 같은것이며 이 부등식은 모든 수학 분야에서 성립한다

내적 연산의 Distance

코시-슈바르츠 부등식에 이어서, 실질적으로 크기 비교를 하기 위해선 Distance에 대한 정의가 필요하다.
수학 분야에서 Distance를 정의하는 방법은 굉장히 다양하다.
벡터 공간과, 내적 연산이라는 정의 안에서 우리는 Distance를 다음과 같이 정의한다.

\[d(x, y) := \lVert x - y \rVert = \sqrt{\langle x - y, x- y \rangle}\]

만약 내적이 dot product라면 이때의 Distance는 Euclidean distance라 불린다.

각과 직교성 (Angles and Orthogonality)

각 (Angle)

벡터 x, 벡터 y가 모두 \(\overrightarrow{0}\)가 아니라면

\[-1 \leq {\langle x, y \rangle \over \lVert x \rVert \lVert y \rVert} \leq 1\]

위 부등식은 코시-슈바르츠 부등식에 의해 유도된다.
위 부등식의 범위는 -1 ~ 1 이며 이것은 \(cos \omega\)를 통해 모두 표현 (아래 그래프 참고)할 수 있으며 이 말은 곧 내적 연산을 각(Angle)과 연관지을 수 있다는 의미이다.

• 호도법이 만들어진 근본적 이유는 (호)의 길이를 각(도)로 표현할 수 있는 방법을 찾고자 하는것이었으며 이러한 생각 논리를 이어서 내적 연산을 각, 그리고 (호)의 길이를 나타내는 수와 연관된다고 생각해도 좋을 듯 하다!

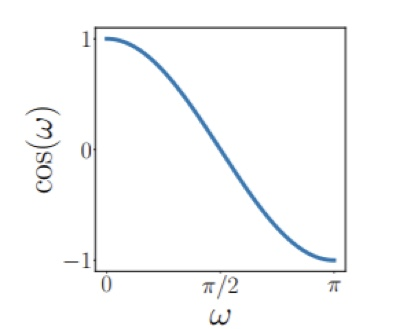
\(sin \omega\) 에는 다른 각에서 동일한 값이 나올 수 있으므로 정확한 표현이 불가능하다.

이 각(Angle)을 이용하면 방향만을 이용해 벡터의 correlation을 측정하는것이 가능하다.

• 벡터를 통한 예시: \(v_1 = (1, 0), v_2 = (100, 0)\) 일 때 두 벡터간의 Distance는 크지만 Angle은 0도이므로 Correlation이 매우 높다고 할 수 있다.
• 실제 적용 예시: 특정 한 사람의 Face를 Detection하는 작업을 한다고 할 때 밝은 사진과 어두운 사진이 있다고 하자. 조명 밝기 차이로 인해 두 사진을 통해 추출된 두 피쳐벡터간 Distance는 매우 클 것이다. 하지만 피부색은 동일하므로 Correlation을 활용하면 두 사진에 동일 인물이 있다고 결론을 내릴 수 있게된다.

직교성(Orthogonality)

Orthogonal matrix는 Angle, Distance 보존 한다.

Orthogonal vectors

\(orthogonal \Leftrightarrow \langle x, y \rangle = 0\) 임.
이때 두 벡터 x, y의 크기가 1 이라면 orthonormal

Orthogonal matrix

matrix를 이루는 모든 column이 orthonormal(orthogonal 아님 주의. 즉 크기까지 1인) 벡터인 경우

\(AA^T = I = A^TA\) 이며 이는 \(A^{-1} = A^T\) 를 의미한다.

Linearly separable data VS Non-linearly separable data

흔히 하는 오해

• Linear Classifier는 Linearly separable data만 분류 가능하고, Non linear Classifier는 Non-linearly separable data만 분류 가능하다?
  • 그렇지 않다. 정해진 건 없다

Linearly separable data

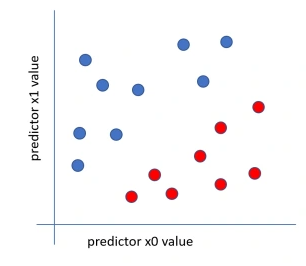
• 2차원 데이터가 있다고 가정할 때 하나의 직선으로 분류 가능한 데이터

Non-linearly separable data

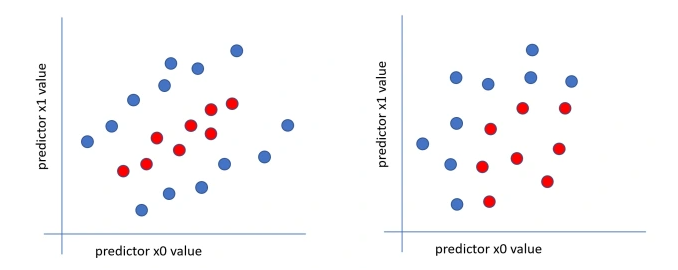
• 하나의 직선으로 구분이 불가능한 데이터(위 그림에서 좌. 두 개의 직선 필요, 우. 곡선 필요)

Linear classifier vs Non-linear classifier

Linear classifier

• 데이터와 가중치(predictable variables)의 선형결합 이용
• 예시
  • 로지스틱 회귀
    • $P = {1.0 \over(1.0 + exp(-z))}$ 임. 이때 $z = w_0x_0 + w_1x_1 + b$로 데이터와 가중치가 선형결합으로 이루어져 있으므로 Linear classifier
    • 로지스틱 회귀 방정식 자체는 비선형이지만 그 비선형방정식 안에서 가중치와 데이터가 선형결합으로 이루어져있어서 Linear classifier이다
      • 비선형 방정식으로 셋팅은 되어있고, 데이터와 가중치를 선형결합해서 셋팅되어있는 함수에 넣어주면 끝임. 즉 쉬움

Non-linear classifier

• 데이터와 가중치(predictable variables)가 선형결합이 아님. 제곱, 제곱근, sines 등과 같은게 들어가있음
• 예시
  • Neural networks, K-nearest neighbors, Decision Tree

선형과 비선형이란?

딥러닝 공부를 하면서 서적이든 인터넷 지식이든 선형, 비선형에 대한 개념만 많이 있고 근본적인 개념을 그림과 함께 명확하게 설명해주는 자료가 없어서 이 답답함을 해소하는데 정말 오랜시간이 걸렸다. (내 구글링 실력이 미천했던 것일수도 있고..)

가장 큰 도움을 준 사이트이다. 참고 답변 사이트

본인이 딥러닝에서의 선형, 비선형 개념이 명확한지 모르겠다면 다음의 질문에 답을 해보자.

단일 퍼셉트론에서 활성화 함수로 Sigmoid 함수, 혹은 Step 함수를 사용한다고 하면 이 퍼셉트론은 Linear-Classifier인가? 혹은 Non-Linear-Classifier인가?

Decision Boundary의 모양을 봐야한다!

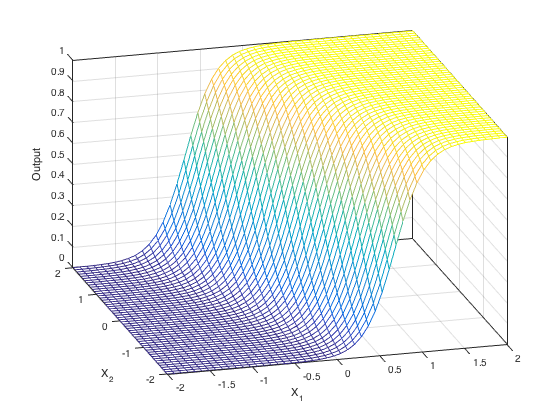
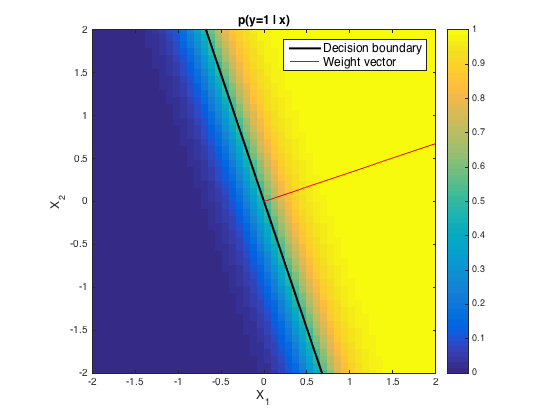
왜 weight vector가 Decision boundary에 orthogonal 한 것인지 자료 찾고 작성 예정