본 포스트는 전통적인 최적화 방법(머신러닝 기반)을 공부하고자 제작했습니다.
전체 내용은 유튜버 혁펜하임님의 강의를 참고했습니다.

최적화 기본 요소

1. 목적함수(Object Function)
   • 어떤 함수를 최소화 or 최대화 하는가?
2. 변수(Decision Variable or Unknown)
   • 어떤 변수를 활용해서 목적함수를 최소화 or 최대화 시키겠는가?
3. 제약 조건(Constraints)

최적화 과정

1. 최적화 기본 3요소를 정의(Identify) => 모델링
2. 최적해 찾기 (이때 다양한 Optimization 함수가 사용될 수 있음)

최적화 기본요소와 과정을 알았다. 그럼 어떻게 목적 함수를 최소화 시킬 수 있을까?

1. 독립 변수 x 가 입력으로 들어왔을 때 \({df \over dx} = 0\) 인지 확인해야 한다.
   • 위 조건은 독립 변수 값 x가 최소가 되기 위한 기본 조건 중 하나이다.

   • 단일 변수의 경우

     \[{df(x) \over dx} = 0\]

   • 다변수일 경우

     \[{\partial f(x_1, x_2, \cdots , x_N) \over \partial x_1}\] \[{\partial f(x_1, x_2, \cdots , x_N) \over \partial x_2}\] \[\vdots\] \[{\partial f(x_1, x_2, \cdots , x_N) \over \partial x_N}\]
   • 위 경우들을 간단하게 그레디언트(gradient) 벡터¹ \(\bigtriangledown f = 0\) 으로 나타내기도 한다.

2. 1번만으론 x 값이 목적함수를 최솟값으로 만드는지, 최댓값으로 만드는지 알 수 없다. 이를 알기 위해선 2차도함수 값이 양수인지 알아야 한다.

3. 최솟값이라고 해도 그 위치가 지역적 최솟값인지 전역적 최솟값인지 알 수 없다. 이 문제에 대한 명시적인 해결 방안은 아직 없으며, 하이퍼 파라미터의 조정 등을 통해 최대한 지역적 최솟값에 빠지지 않기 위해 실험을 진행한다.

대표적 Convex Optimization: SVM

• SVM은 뭐다? 국경만들기

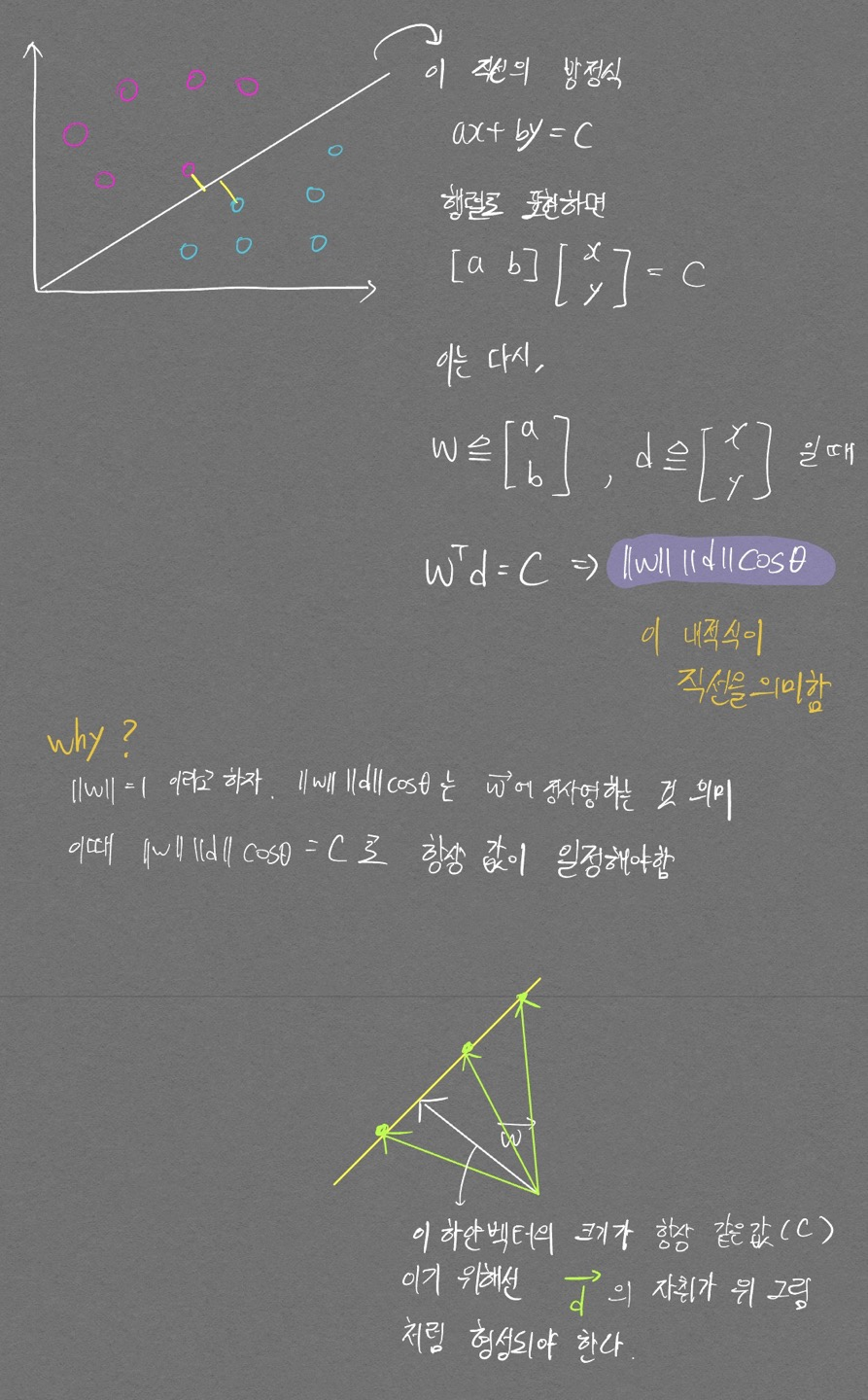
이제 최적화에 필요한 기본요소를 모두 얻었다.

1. 목적함수

\[min(w^Tw)\]

1. 제약조건

\[w^Td_i >= c + 1 (i는 분홍색)\] \[w^Td_i < c - 1 (i는 파란색)\]

이제 목적함수에 미분을 취해서 0이 되는 지점을 찾으면 되지만, 추후에 직접 미분까지 진행해보도록 하자.