논문 이해를 위한 Source
Method
- Make a memory bank of patch features
- Memory bank:
- 쓰는 이유: middle level of feature 들을 사용하기 위함
- Reduce the memory bank with coreset
- Detect anomaly with the memory bank
수식 이해
\[\phi_{i, j} = \phi_j(x_i) \in R^{c^* \times h^* \times w^*}\]- \(\phi_{i, j}\)는 결국 Pretrained model의 정상데이터 i에 대한 j번째 layer의
feature이다.
- 좌표 정보 \((h, w)\) 를 주면 \(c^*\) 차원을 가진 vector 들을 얻을 수 있음.
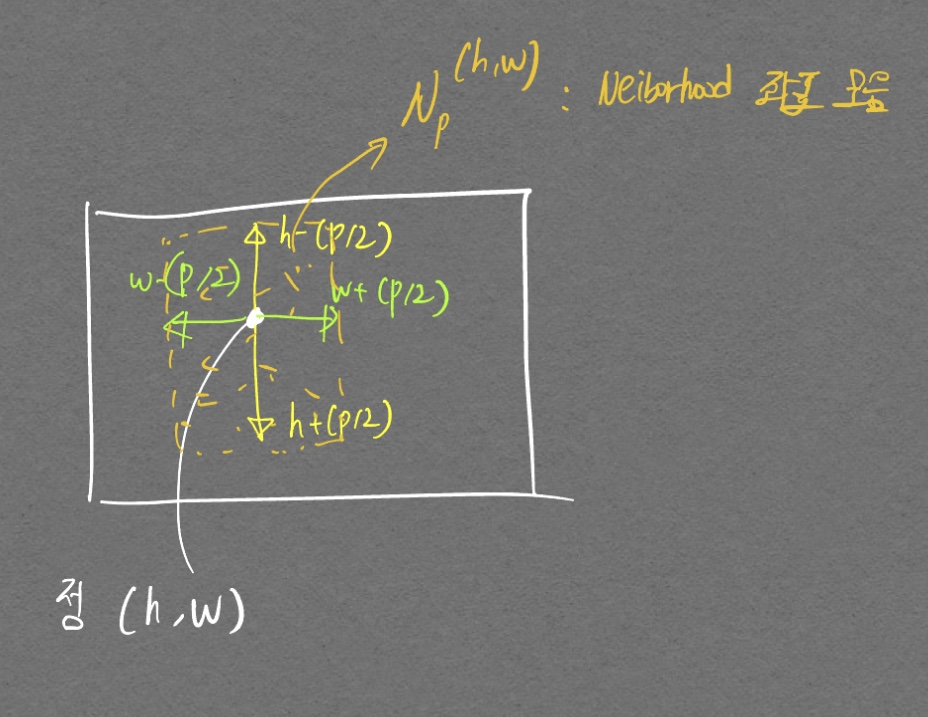
(h, w) 좌표 기준 주변 좌표들의 모음이다.
- 즉 (h, w) 좌표 주변부 픽셀들에 대한 \(c^*\) 차원 feature vector들을 가리키는 말이다. 이때 \(f_{agg}\) 에서 Adaptive average pooling1을 사용하여 나오는 feature 수를 제한함.
- channel에 대해서 pooling을 하는것인지, height width에 대해 pooling을 하는것인지 아직 잘 모르겠다. (channel에 대한 pooling인 듯하다)
- \(P_{s, p}(\phi_{i, j})\)는 여러 좌표에서의 neightbood feature vector들을 가지고 있는
하나의 patch라고 생각하면 될 듯 하다.
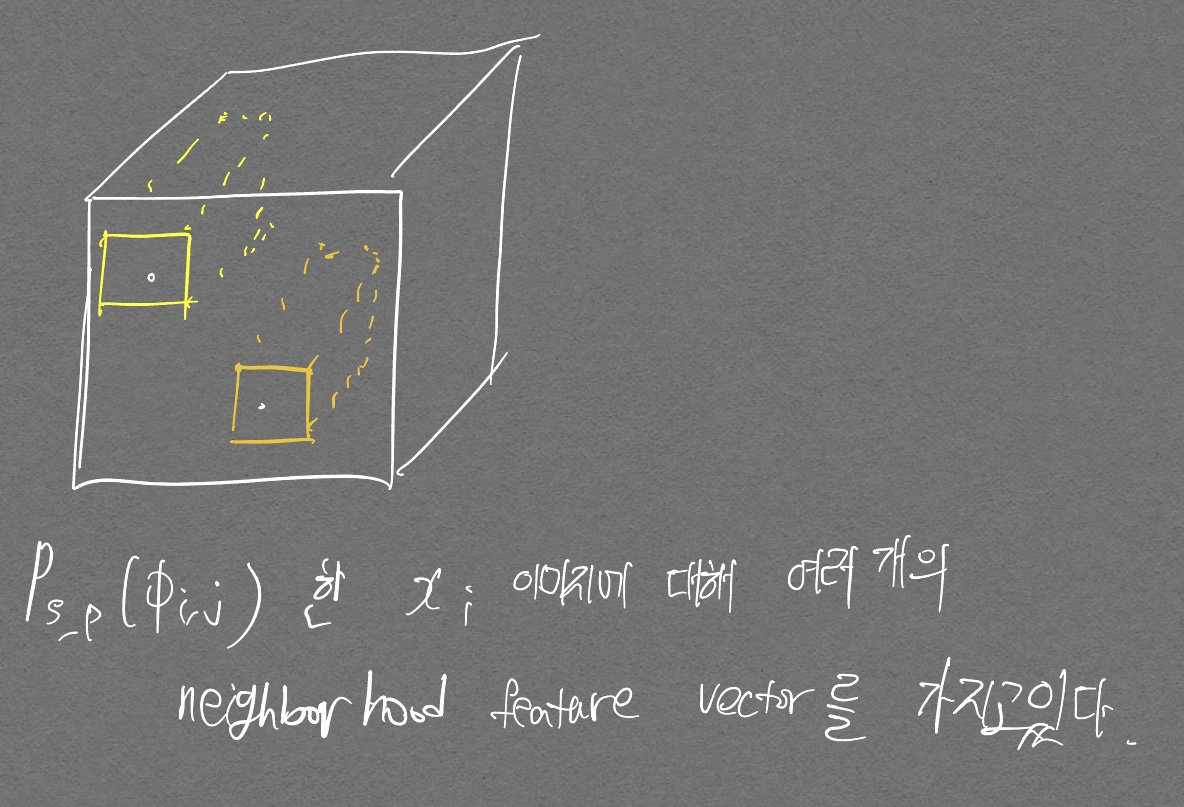
- patch를 모은것이 \(M\) (메모리 뱅크)이다.
-
Average pooling은 이미지의 크기에 따라서 Tensor 크기가 달라지지만 Adaptive average pooling은 원하는 output Tensor를 고정할 수 있다 Pytorch 링크. ↩
PREVIOUS경제