본 포스터는 3치원 Point Cloud 데이터에 대한 도메인과 Projection(정사영) 이론 및 코드 실습을 정리한 것입니다. 다크 프로그래머님의 [영상 Geometry]글을 참고했습니다.
포인트 클라우드 데이터 기본 지식
작성 예정
카메라 캘리브레이션
카메라의 내부 파라미터(Intrinsic Parameter)를 구하는 과정이다.
본 포스터를 이해하기 위해선 아래 좌표계 목록부터 차근차근 보는것을 추천한다.
좌표계
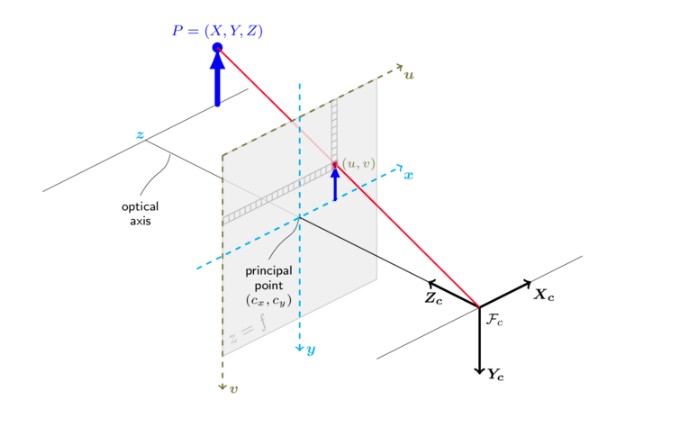
출처: https://gaussian37.github.io/vision-depth-pcd_depthmap
원래 영상 좌표계의 시작점은 왼쪽 모서리 상단이다.
그러나 위 그림은 이미 주점을 통해 영상 좌표계를 이동시켜준 것으로 생각하면 편하다.
이동 안해줬다면 x, y축과 u, v축이 서로 바뀌었어야함.
영상 기하학에는 4가지 좌표계 존재.
월드 좌표계(World Coordinate System)
공간상의 한 지점을 기준으로 한 좌표계.
3차원
카메라 좌표계(Camera Coordinate System)
공간상에서 카메라를 기준으로 한 좌표계.
3차원
영상 좌표계(Image Coordinate System)
우리가 실제 눈으로 보는 이미지에 대한 좌표계.
2차원
정규 좌표계(Normalized Image Coordinate System)
영상 좌표계에서 카메라의 내부 파라미터 영향을 제거한 좌표계.
2차원
카메라마다 고유의 특징이 존재해서 기하학적으로 이미지를 해석하기 어려울 수 있기에, 이것과 관련한 카메라 내부 파라미터 영향을 제거해서 기하학적 해석을 쉽게 하기 위함.
카메라 내부 파라미터를 알면 정규 좌표계 -> 영상 좌표계로의 변환 가능.
\[\begin{bmatrix} x \\ y \\ 1\end{bmatrix} = \begin{bmatrix} f_x & skew\_cf_x & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} u \\ v \\ 1 \end{bmatrix}\]\(x, y\): 영상 좌표계의 좌표 정보
\(u, v\): 정규 좌표계의 좌표 정보
\(f_x, f_y\): 초점거리1 -> 카메라 렌즈의 중점과 이미지 센서간의 거리
\(c_x, c_y\): 주점(Principal Point)2 -> 카메라 렌즈에서 이미지 센서로 내린 수선의 발(교점) 좌표
\(skew \_ cf_x\): 비대칭 계수3
카메라 내부 파라미터
수식(1)의 초점 거리, 주점, 비대칭계수가 카메라의 내부 파라미터이다.
카메라 외부 파라미터
카메라 좌표계, 월드 좌표계 사이의 변환 관계를 설명하는 파라미터이다.
동차 좌표계(Homogeneous Coordinates)
어떤 목적을 위해 좌표계에 하나의 차원을 추가해서 새롭게 표현한 좌표계를 동차 좌표계라고 함. 다양한 도메인에 따라 그 목적이 달라지겠지만, 여기서는 카메라 영상처리 관련한 부분이니 카메라 도메인을 접목시켜서 설명해보면 다음과 같다.
World Coordinate -> Image Coordinate로 변환할 때 여러 모든 점이 동일한 Image Coordinate로 표현될 수 있다.
이러한 모든 점을 한번에 표현하기 위함이다.
Image Coordinate 좌표 (u, v)의 동차 좌표는 (u, v, 1)이다.
그림으로 보면 이해가 더 쉽다.
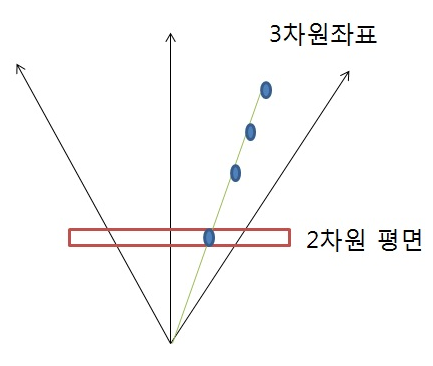
이러한 관점에서 볼 때, 동차 좌표(x, y, z)에서 (x/z, y/z)를 구하는 것은 Projection이며
(u, v)를 동차 좌표(wu, wv, w)로 표현하는 것은 Inverse Projection으로 볼 수 있다.
이 외에도 동차 좌표계를 사용하는 이유는 다양하다.
Affine Transformation과 같이 선형 변환 + 이동으로 정의된 변환은 y = Ax + b 꼴 이므로 선형 변환이 아니게 된다.
이때 동차 좌표계 개념을 사용하면 선형변환 y = Ax 꼴로 바꿔줄 수 있으며, 자세한 내용은 추후 정리하기로 하자. (외적, 다크프로그래머님 직선의 방정식 고찰 등)
3D -> 2D로 Projection 할 때
- 보존되는 정보
- 선의 Type: 직선은 직선으로 투영되고, 곡선은 곡선으로 투영된다.
- 포함 관계: 추후 정리 필요
- 잃는 정보
- 길이
- 각도
- 평행성: 3D -> 2D로 Projection 하는 것을 2차원 사영 기하학(Projection Geometry)이라고 하며, 여기선 평행한 두 선의 교점을 구할 수 있다.

Python 코드 실습
-
카메라 좌표계를 기준으로 하나의 점이 공간상에 존재할 때, 이를 영상 좌표계로 변환하는 코드
import numpy as np if __name__ == '__main__': X = np.array([20, 30, 40]).T z = X[2] K = np.array( [ [10, 0, 20], [0, 20, 40], [0, 0, 1] ] ) # camera coordinate -> normalized uv plane # homogeneous coorindate system!! uv_norm = X / z print(uv_norm) # normalized uv plane -> uv plane uv = np.dot(K, uv_norm) uv = uv.astype(np.uint8) print(uv) # uv plane -> normalized uv plane uv_norm = np.dot(np.linalg.inv(K), uv) # linalg.inv: 선형대수학 역변환! print(uv_norm) # normalized uv plane -> camera coordinate X = z * uv_norm print(X)X: 3차원 공간에서 카메라를 기준으로 x, y, z축이 존재한다고 할 때(즉, 카메라의 중점이 0, 0, 0 이라고 생각하면 됨) 하나의 점이 \(\begin{bmatrix}20\\30\\40\end{bmatrix}\)에 위치해 있는 것임K: 카메라 내부 파라미터 정보- 스칼라
c, 행렬A,B가 있을 경우 스칼라와 행렬끼리의 곱은 교환법칙이 성립한다. -cA==Ac이고, 행렬끼리의 분배법칙은 성립하므로 (cA)B == (Ac)B - 행렬끼리의 분배법칙이 성립한다는 것은 (AB)C == A(BC)임을 의미한다.
-
여러 PCD 데이터에 대해서 영상 좌표계 값 구하기
import numpy as np if __name__ == '__main__': X = np.array([ [20, 30, 40], [10, 30, 80], [25, 12, 90], [30, 10, 100], [50, 30, 40] ]).T K = np.array([ [10, 0, 20], [0, 20, 40], [0, 0, 1] ]) print(X) print(X[2, :]) uv = (1/X[2, :] * np.dot(K, X)) uv = uv.astype(np.uint8) print(uv.T)
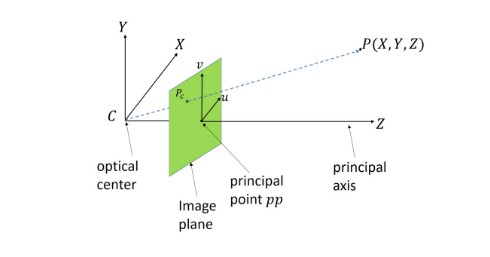 주점이 필요한 이유: 이미지 센서의 좌표(x, y)는 시작점이 가운데 지점이 아닌 왼쪽 모서리 상단 부분이다. 따라서 정확한 좌표를 얻기 위해선 마지막에 주점을 더해주는 작업이 필요하다. 그래서
주점이 필요한 이유: 이미지 센서의 좌표(x, y)는 시작점이 가운데 지점이 아닌 왼쪽 모서리 상단 부분이다. 따라서 정확한 좌표를 얻기 위해선 마지막에 주점을 더해주는 작업이 필요하다. 그래서