문제
- 미국 아이오와 주의 에임스(Ames) 지방의 주택 가격 정보를 알아보는 회귀 문제
- 성능 평가는 RMSLE(Root Mean Squared Log Error)로 진행됨
- 가격이 비싼 주택일수록 예측 결과 오류가 전체 오류에 미치는 비중이 커지므로 이를 상쇄하기 위해 오류 값을 로그 변환한 RMSLE로 사용함
데이터 사전 처리(Preprocessing)
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
house_df_org = pd.read_csv('house_price.csv')
house_df = house_df_org.copy()
house_df.head(3)
| Id | MSSubClass | MSZoning | LotFrontage | LotArea | Street | Alley | LotShape | LandContour | Utilities | ... | PoolArea | PoolQC | Fence | MiscFeature | MiscVal | MoSold | YrSold | SaleType | SaleCondition | SalePrice | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 60 | RL | 65.0 | 8450 | Pave | NaN | Reg | Lvl | AllPub | ... | 0 | NaN | NaN | NaN | 0 | 2 | 2008 | WD | Normal | 208500 |
| 1 | 2 | 20 | RL | 80.0 | 9600 | Pave | NaN | Reg | Lvl | AllPub | ... | 0 | NaN | NaN | NaN | 0 | 5 | 2007 | WD | Normal | 181500 |
| 2 | 3 | 60 | RL | 68.0 | 11250 | Pave | NaN | IR1 | Lvl | AllPub | ... | 0 | NaN | NaN | NaN | 0 | 9 | 2008 | WD | Normal | 223500 |
3 rows × 81 columns
house_df.isnull().sum(axis=0)
Id 0
MSSubClass 0
MSZoning 0
LotFrontage 259
LotArea 0
...
MoSold 0
YrSold 0
SaleType 0
SaleCondition 0
SalePrice 0
Length: 81, dtype: int64
print('데이터 세트의 Shape:', house_df.shape)
print('\n전체 feature 들의 type \n',house_df.dtypes.value_counts())
isnull_series = house_df.isnull().sum()
print('\nNull 컬럼과 그 건수:\n ', isnull_series[isnull_series > 0].sort_values(ascending=False)) # isnull_series중 0보다 큰 것들을 선택하는 것.
# isnull_series가 데이터프레임이면, 불린 인덱싱으로 시리즈를 줬으므로 isnull_series중 선택할 행을 고른다
데이터 세트의 Shape: (1460, 81)
전체 feature 들의 type
object 43
int64 35
float64 3
dtype: int64
Null 컬럼과 그 건수:
PoolQC 1453
MiscFeature 1406
Alley 1369
Fence 1179
FireplaceQu 690
LotFrontage 259
GarageType 81
GarageYrBlt 81
GarageFinish 81
GarageQual 81
GarageCond 81
BsmtExposure 38
BsmtFinType2 38
BsmtFinType1 37
BsmtCond 37
BsmtQual 37
MasVnrArea 8
MasVnrType 8
Electrical 1
dtype: int64
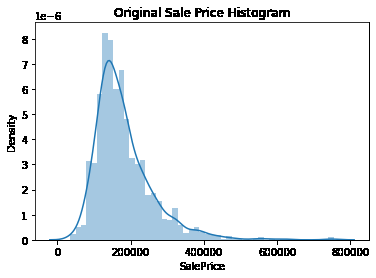
plt.title('Original Sale Price Histogram')
sns.distplot(house_df['SalePrice'])
# house_df['SalePrice'].hist() # 이걸로도 시각화 가능
<AxesSubplot:title={'center':'Original Sale Price Histogram'}, xlabel='SalePrice', ylabel='Density'>
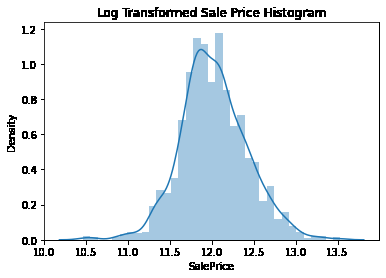
plt.title('Log Transformed Sale Price Histogram')
log_SalePrice = np.log1p(house_df['SalePrice'])
sns.distplot(log_SalePrice)
<AxesSubplot:title={'center':'Log Transformed Sale Price Histogram'}, xlabel='SalePrice', ylabel='Density'>
# SalePrice 로그 변환
original_SalePrice = house_df['SalePrice']
house_df['SalePrice'] = np.log1p(house_df['SalePrice'])
# Null 이 너무 많은 컬럼들과 불필요한 컬럼 삭제
house_df.drop(['Id','PoolQC' , 'MiscFeature', 'Alley', 'Fence','FireplaceQu'], axis=1 , inplace=True)
# Drop 하지 않는 숫자형 Null컬럼들은 평균값으로 대체
house_df.fillna(house_df.mean(),inplace=True)
# Null 값이 있는 피처명과 타입을 추출
null_column_count = house_df.isnull().sum()[house_df.isnull().sum() > 0]
print('## Null 피처의 Type :\n', house_df.dtypes[null_column_count.index])
## Null 피처의 Type :
MasVnrType object
BsmtQual object
BsmtCond object
BsmtExposure object
BsmtFinType1 object
BsmtFinType2 object
Electrical object
GarageType object
GarageFinish object
GarageQual object
GarageCond object
dtype: object
print('get_dummies() 수행 전 데이터 Shape:', house_df.shape)
house_df_ohe = pd.get_dummies(house_df)
print('get_dummies() 수행 후 데이터 Shape:', house_df_ohe.shape)
null_column_count = house_df_ohe.isnull().sum()[house_df_ohe.isnull().sum() > 0]
print('## Null 피처의 Type :\n', house_df_ohe.dtypes[null_column_count.index])
get_dummies() 수행 전 데이터 Shape: (1460, 75)
get_dummies() 수행 후 데이터 Shape: (1460, 271)
## Null 피처의 Type :
Series([], dtype: object)
선형 회귀 모델의 학습/예측/평가
def get_rmse(model):
pred = model.predict(X_test)
mse = mean_squared_error(y_test , pred)
rmse = np.sqrt(mse)
print('{0} 로그 변환된 RMSE: {1}'.format(model.__class__.__name__,np.round(rmse, 3)))
return rmse
def get_rmses(models):
rmses = [ ]
for model in models:
rmse = get_rmse(model)
rmses.append(rmse)
return rmses
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
y_target = house_df_ohe['SalePrice']
X_features = house_df_ohe.drop('SalePrice',axis=1, inplace=False)
X_train, X_test, y_train, y_test = train_test_split(X_features, y_target, test_size=0.2, random_state=156)
# LinearRegression, Ridge, Lasso 학습, 예측, 평가
lr_reg = LinearRegression()
lr_reg.fit(X_train, y_train)
ridge_reg = Ridge()
ridge_reg.fit(X_train, y_train)
lasso_reg = Lasso()
lasso_reg.fit(X_train, y_train)
models = [lr_reg, ridge_reg, lasso_reg]
get_rmses(models)
LinearRegression 로그 변환된 RMSE: 0.132
Ridge 로그 변환된 RMSE: 0.128
Lasso 로그 변환된 RMSE: 0.176
[0.1318957657915422, 0.12750846334053031, 0.17628250556471395]
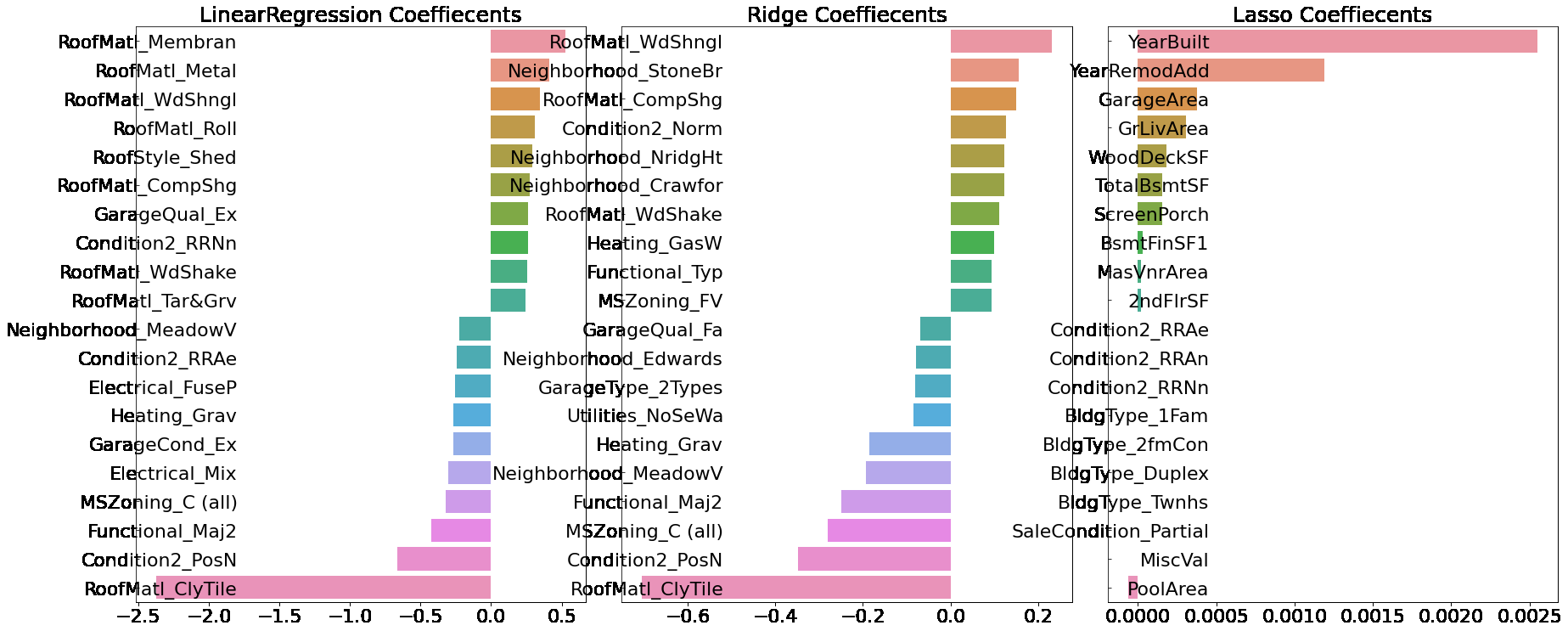
def get_top_bottom_coef(model):
# coef_ 속성을 기반으로 Series 객체를 생성. index는 컬럼명.
coef = pd.Series(model.coef_, index=X_features.columns)
# + 상위 10개 , - 하위 10개 coefficient 추출하여 반환.
coef_high = coef.sort_values(ascending=False).head(10)
coef_low = coef.sort_values(ascending=False).tail(10)
return coef_high, coef_low
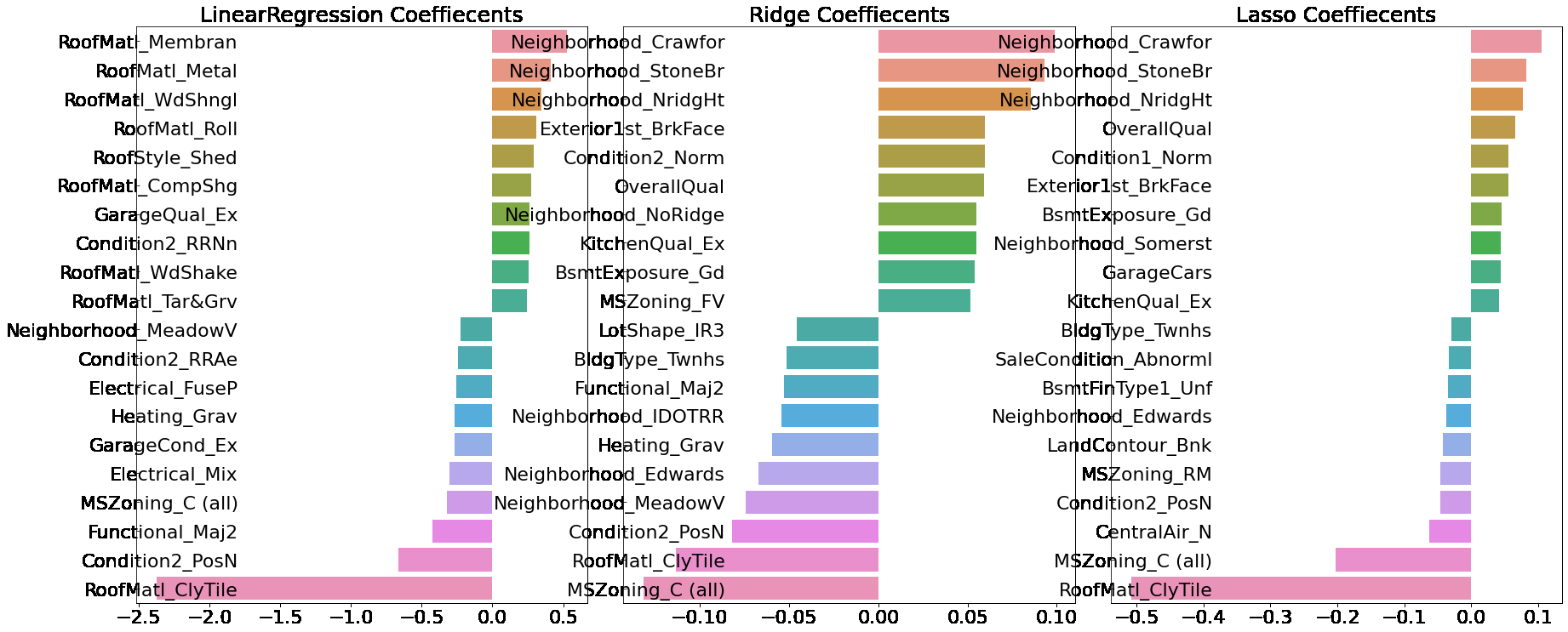
def visualize_coefficient(models):
# 3개 회귀 모델의 시각화를 위해 3개의 컬럼을 가지는 subplot 생성
fig, axs = plt.subplots(figsize=(24,10),nrows=1, ncols=3)
fig.tight_layout()
# 입력인자로 받은 list객체인 models에서 차례로 model을 추출하여 회귀 계수 시각화.
for i_num, model in enumerate(models):
# 상위 10개, 하위 10개 회귀 계수를 구하고, 이를 판다스 concat으로 결합.
coef_high, coef_low = get_top_bottom_coef(model)
coef_concat = pd.concat( [coef_high , coef_low] )
# 순차적으로 ax subplot에 barchar로 표현. 한 화면에 표현하기 위해 tick label 위치와 font 크기 조정.
axs[i_num].set_title(model.__class__.__name__+' Coeffiecents', size=25)
axs[i_num].tick_params(axis="y",direction="in", pad=-120)
for label in (axs[i_num].get_xticklabels() + axs[i_num].get_yticklabels()):
label.set_fontsize(22)
sns.barplot(x=coef_concat.values, y=coef_concat.index , ax=axs[i_num])
# 앞 예제에서 학습한 lr_reg, ridge_reg, lasso_reg 모델의 회귀 계수 시각화.
models = [lr_reg, ridge_reg, lasso_reg]
visualize_coefficient(models)
from sklearn.model_selection import cross_val_score
def get_avg_rmse_cv(models):
for model in models:
# 분할하지 않고 전체 데이터로 cross_val_score( ) 수행. 모델별 CV RMSE값과 평균 RMSE 출력
rmse_list = np.sqrt(-cross_val_score(model, X_features, y_target,
scoring="neg_mean_squared_error", cv = 5))
rmse_avg = np.mean(rmse_list)
print('\n{0} CV RMSE 값 리스트: {1}'.format( model.__class__.__name__, np.round(rmse_list, 3)))
print('{0} CV 평균 RMSE 값: {1}'.format( model.__class__.__name__, np.round(rmse_avg, 3)))
# 앞 예제에서 학습한 lr_reg, ridge_reg, lasso_reg 모델의 CV RMSE값 출력
models = [lr_reg, ridge_reg, lasso_reg]
get_avg_rmse_cv(models)
LinearRegression CV RMSE 값 리스트: [0.135 0.165 0.168 0.111 0.198]
LinearRegression CV 평균 RMSE 값: 0.155
Ridge CV RMSE 값 리스트: [0.117 0.154 0.142 0.117 0.189]
Ridge CV 평균 RMSE 값: 0.144
Lasso CV RMSE 값 리스트: [0.161 0.204 0.177 0.181 0.265]
Lasso CV 평균 RMSE 값: 0.198
- 하이퍼 파라미터 튜닝
from sklearn.model_selection import GridSearchCV
def print_best_params(model, params):
grid_model = GridSearchCV(model, param_grid=params,
scoring='neg_mean_squared_error', cv=5)
grid_model.fit(X_features, y_target)
rmse = np.sqrt(-1* grid_model.best_score_)
print('{0} 5 CV 시 최적 평균 RMSE 값: {1}, 최적 alpha:{2}'.format(model.__class__.__name__,
np.round(rmse, 4), grid_model.best_params_))
return grid_model.best_estimator_
ridge_params = { 'alpha':[0.05, 0.1, 1, 5, 8, 10, 12, 15, 20] }
lasso_params = { 'alpha':[0.001, 0.005, 0.008, 0.05, 0.03, 0.1, 0.5, 1,5, 10] }
best_rige = print_best_params(ridge_reg, ridge_params)
best_lasso = print_best_params(lasso_reg, lasso_params)
Ridge 5 CV 시 최적 평균 RMSE 값: 0.1418, 최적 alpha:{'alpha': 12}
Lasso 5 CV 시 최적 평균 RMSE 값: 0.142, 최적 alpha:{'alpha': 0.001}
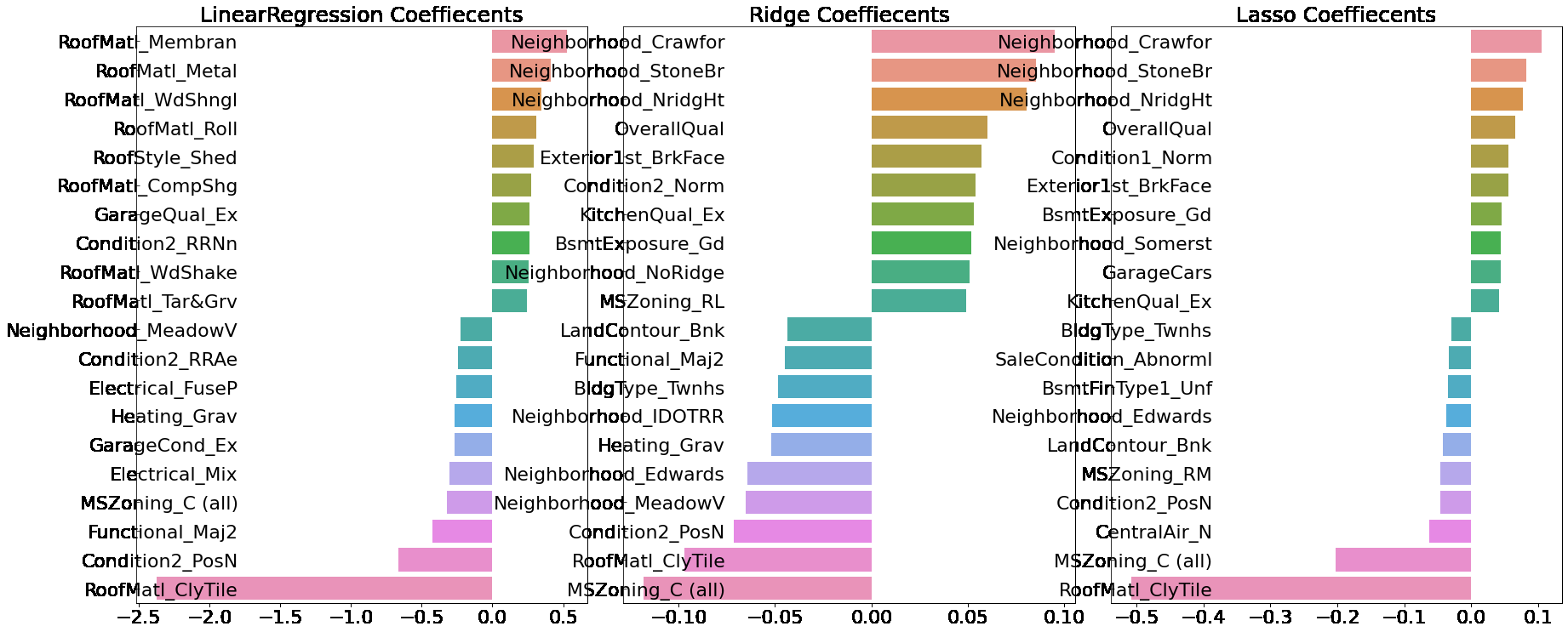
# 앞의 최적화 alpha값으로 학습데이터로 학습, 테스트 데이터로 예측 및 평가 수행.
lr_reg = LinearRegression()
lr_reg.fit(X_train, y_train)
ridge_reg = Ridge(alpha=12)
ridge_reg.fit(X_train, y_train)
lasso_reg = Lasso(alpha=0.001)
lasso_reg.fit(X_train, y_train)
# 모든 모델의 RMSE 출력
models = [lr_reg, ridge_reg, lasso_reg]
get_rmses(models)
# 모든 모델의 회귀 계수 시각화
models = [lr_reg, ridge_reg, lasso_reg]
visualize_coefficient(models)
LinearRegression 로그 변환된 RMSE: 0.132
Ridge 로그 변환된 RMSE: 0.124
Lasso 로그 변환된 RMSE: 0.12
- 데이터 왜곡 로그 변환 후 성능 평가
from scipy.stats import skew
# object가 아닌 숫자형 피쳐의 컬럼 index 객체 추출.
features_index = house_df.dtypes[house_df.dtypes != 'object'].index
# house_df에 컬럼 index를 [ ]로 입력하면 해당하는 컬럼 데이터 셋 반환. apply lambda로 skew( )호출
skew_features = house_df[features_index].apply(lambda x : skew(x))
print(house_df[features_index])
# skew 정도가 1 이상인 컬럼들만 추출.
skew_features_top = skew_features[skew_features > 1]
print(skew_features_top.sort_values(ascending=False))
MSSubClass LotFrontage LotArea OverallQual OverallCond YearBuilt \
0 60 65.0 8450 7 5 2003
1 20 80.0 9600 6 8 1976
2 60 68.0 11250 7 5 2001
3 70 60.0 9550 7 5 1915
4 60 84.0 14260 8 5 2000
... ... ... ... ... ... ...
1455 60 62.0 7917 6 5 1999
1456 20 85.0 13175 6 6 1978
1457 70 66.0 9042 7 9 1941
1458 20 68.0 9717 5 6 1950
1459 20 75.0 9937 5 6 1965
YearRemodAdd MasVnrArea BsmtFinSF1 BsmtFinSF2 ... WoodDeckSF \
0 2003 196.0 706 0 ... 0
1 1976 0.0 978 0 ... 298
2 2002 162.0 486 0 ... 0
3 1970 0.0 216 0 ... 0
4 2000 350.0 655 0 ... 192
... ... ... ... ... ... ...
1455 2000 0.0 0 0 ... 0
1456 1988 119.0 790 163 ... 349
1457 2006 0.0 275 0 ... 0
1458 1996 0.0 49 1029 ... 366
1459 1965 0.0 830 290 ... 736
OpenPorchSF EnclosedPorch 3SsnPorch ScreenPorch PoolArea MiscVal \
0 61 0 0 0 0 0
1 0 0 0 0 0 0
2 42 0 0 0 0 0
3 35 272 0 0 0 0
4 84 0 0 0 0 0
... ... ... ... ... ... ...
1455 40 0 0 0 0 0
1456 0 0 0 0 0 0
1457 60 0 0 0 0 2500
1458 0 112 0 0 0 0
1459 68 0 0 0 0 0
MoSold YrSold SalePrice
0 2 2008 12.247699
1 5 2007 12.109016
2 9 2008 12.317171
3 2 2006 11.849405
4 12 2008 12.429220
... ... ... ...
1455 8 2007 12.072547
1456 2 2010 12.254868
1457 5 2010 12.493133
1458 4 2010 11.864469
1459 6 2008 11.901590
[1460 rows x 37 columns]
MiscVal 24.451640
PoolArea 14.813135
LotArea 12.195142
3SsnPorch 10.293752
LowQualFinSF 9.002080
KitchenAbvGr 4.483784
BsmtFinSF2 4.250888
ScreenPorch 4.117977
BsmtHalfBath 4.099186
EnclosedPorch 3.086696
MasVnrArea 2.673661
LotFrontage 2.382499
OpenPorchSF 2.361912
BsmtFinSF1 1.683771
WoodDeckSF 1.539792
TotalBsmtSF 1.522688
MSSubClass 1.406210
1stFlrSF 1.375342
GrLivArea 1.365156
dtype: float64
- 위 코드에서 카테고리 피처는 코드성 피처이므로 인코딩 시 왜곡될 가능성이 높아서 skew()함수 적용할 때 원핫 인코딩이 적용 안됀 house_df 여야 한다고 함 - 아직 왜 그런지 모르겠음..
house_df[skew_features_top.index] = np.log1p(house_df[skew_features_top.index])
# Skew가 높은 피처들을 로그 변환 했으므로 다시 원-핫 인코딩 적용 및 피처/타겟 데이터 셋 생성,
house_df_ohe = pd.get_dummies(house_df)
y_target = house_df_ohe['SalePrice']
X_features = house_df_ohe.drop('SalePrice',axis=1, inplace=False)
X_train, X_test, y_train, y_test = train_test_split(X_features, y_target, test_size=0.2, random_state=156)
# 피처들을 로그 변환 후 다시 최적 하이퍼 파라미터와 RMSE 출력
ridge_params = { 'alpha':[0.05, 0.1, 1, 5, 8, 10, 12, 15, 20] }
lasso_params = { 'alpha':[0.001, 0.005, 0.008, 0.05, 0.03, 0.1, 0.5, 1,5, 10] }
best_ridge = print_best_params(ridge_reg, ridge_params)
best_lasso = print_best_params(lasso_reg, lasso_params)
Ridge 5 CV 시 최적 평균 RMSE 값: 0.1418, 최적 alpha:{'alpha': 12}
Lasso 5 CV 시 최적 평균 RMSE 값: 0.142, 최적 alpha:{'alpha': 0.001}
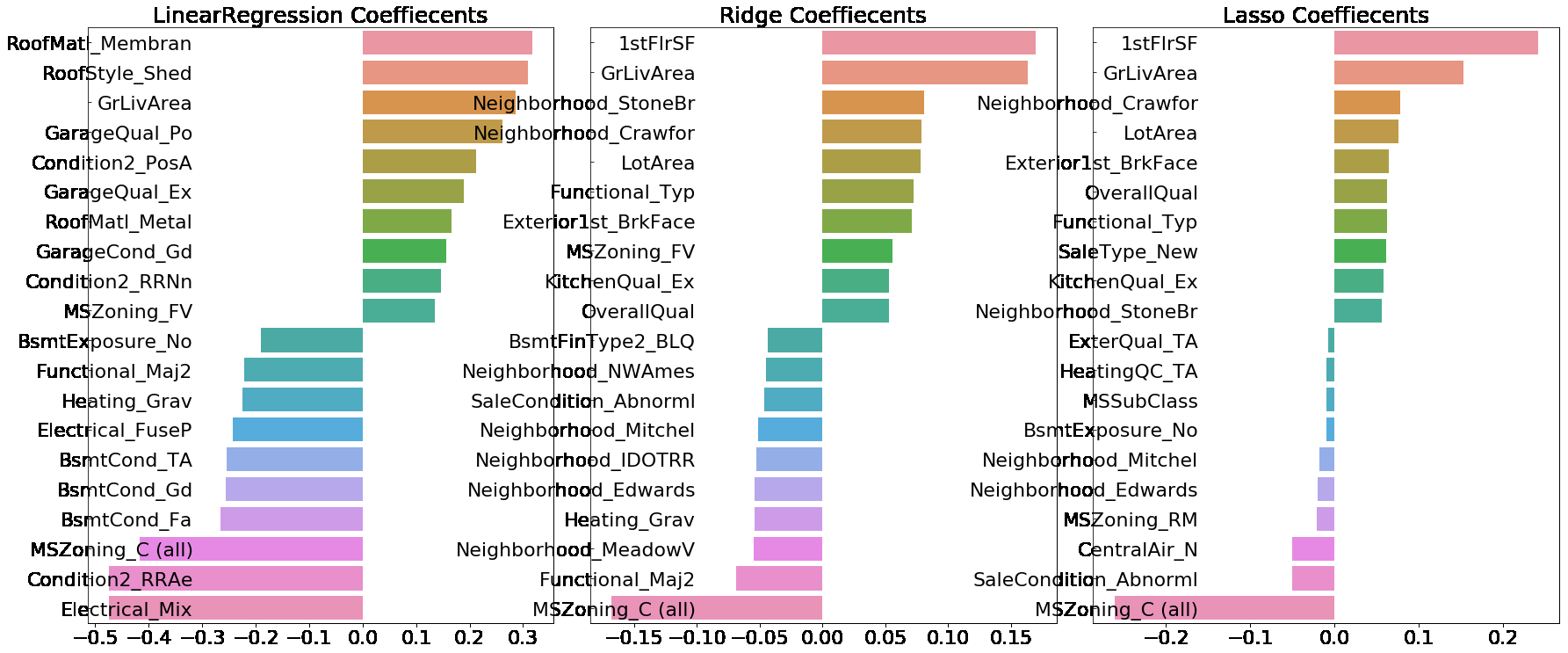
# 앞의 최적화 alpha값으로 학습데이터로 학습, 테스트 데이터로 예측 및 평가 수행.
lr_reg = LinearRegression()
lr_reg.fit(X_train, y_train)
ridge_reg = Ridge(alpha=10)
ridge_reg.fit(X_train, y_train)
lasso_reg = Lasso(alpha=0.001)
lasso_reg.fit(X_train, y_train)
# 모든 모델의 RMSE 출력
models = [lr_reg, ridge_reg, lasso_reg]
get_rmses(models)
# 모든 모델의 회귀 계수 시각화
models = [lr_reg, ridge_reg, lasso_reg]
visualize_coefficient(models)
LinearRegression 로그 변환된 RMSE: 0.132
Ridge 로그 변환된 RMSE: 0.124
Lasso 로그 변환된 RMSE: 0.12
- 이상치 제거
plt.scatter(x = house_df_org['GrLivArea'], y = house_df_org['SalePrice'])
plt.ylabel('SalePrice', fontsize=15)
plt.xlabel('GrLivArea', fontsize=15)
plt.show()
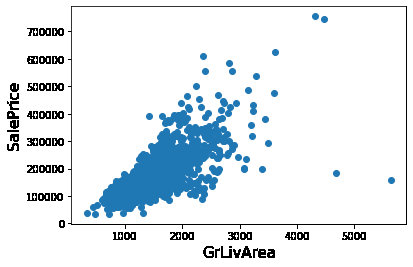
# GrLivArea와 SalePrice 모두 로그 변환되었으므로 이를 반영한 조건 생성.
cond1 = house_df_ohe['GrLivArea'] > np.log1p(4000)
cond2 = house_df_ohe['SalePrice'] < np.log1p(500000)
outlier_index = house_df_ohe[cond1 & cond2].index
print('아웃라이어 레코드 index :', outlier_index.values)
print('아웃라이어 삭제 전 house_df_ohe shape:', house_df_ohe.shape)
# DataFrame의 index를 이용하여 아웃라이어 레코드 삭제.
house_df_ohe.drop(outlier_index , axis=0, inplace=True)
print('아웃라이어 삭제 후 house_df_ohe shape:', house_df_ohe.shape)
아웃라이어 레코드 index : [ 523 1298]
아웃라이어 삭제 전 house_df_ohe shape: (1460, 271)
아웃라이어 삭제 후 house_df_ohe shape: (1458, 271)
y_target = house_df_ohe['SalePrice']
X_features = house_df_ohe.drop('SalePrice',axis=1, inplace=False)
X_train, X_test, y_train, y_test = train_test_split(X_features, y_target, test_size=0.2, random_state=156)
ridge_params = { 'alpha':[0.05, 0.1, 1, 5, 8, 10, 12, 15, 20] }
lasso_params = { 'alpha':[0.001, 0.005, 0.008, 0.05, 0.03, 0.1, 0.5, 1,5, 10] }
best_ridge = print_best_params(ridge_reg, ridge_params)
best_lasso = print_best_params(lasso_reg, lasso_params)
Ridge 5 CV 시 최적 평균 RMSE 값: 0.1125, 최적 alpha:{'alpha': 8}
Lasso 5 CV 시 최적 평균 RMSE 값: 0.1122, 최적 alpha:{'alpha': 0.001}
# 앞의 최적화 alpha값으로 학습데이터로 학습, 테스트 데이터로 예측 및 평가 수행.
lr_reg = LinearRegression()
lr_reg.fit(X_train, y_train)
ridge_reg = Ridge(alpha=8)
ridge_reg.fit(X_train, y_train)
lasso_reg = Lasso(alpha=0.001)
lasso_reg.fit(X_train, y_train)
# 모든 모델의 RMSE 출력
models = [lr_reg, ridge_reg, lasso_reg]
get_rmses(models)
# 모든 모델의 회귀 계수 시각화
models = [lr_reg, ridge_reg, lasso_reg]
visualize_coefficient(models)
LinearRegression 로그 변환된 RMSE: 0.129
Ridge 로그 변환된 RMSE: 0.103
Lasso 로그 변환된 RMSE: 0.1
회귀 트리 학습/예측/평가
from xgboost import XGBRegressor
xgb_params = {'n_estimators':[1000]}
xgb_reg = XGBRegressor(n_estimators=1000, learning_rate=0.05,
colsample_bytree=0.5, subsample=0.8)
best_xgb = print_best_params(xgb_reg, xgb_params)
[15:40:39] WARNING: src/objective/regression_obj.cu:152: reg:linear is now deprecated in favor of reg:squarederror.
[15:40:43] WARNING: src/objective/regression_obj.cu:152: reg:linear is now deprecated in favor of reg:squarederror.
[15:40:47] WARNING: src/objective/regression_obj.cu:152: reg:linear is now deprecated in favor of reg:squarederror.
[15:40:51] WARNING: src/objective/regression_obj.cu:152: reg:linear is now deprecated in favor of reg:squarederror.
[15:40:55] WARNING: src/objective/regression_obj.cu:152: reg:linear is now deprecated in favor of reg:squarederror.
[15:41:00] WARNING: src/objective/regression_obj.cu:152: reg:linear is now deprecated in favor of reg:squarederror.
XGBRegressor 5 CV 시 최적 평균 RMSE 값: 0.115, 최적 alpha:{'n_estimators': 1000}
from lightgbm import LGBMRegressor
lgbm_params = {'n_estimators':[1000]}
lgbm_reg = LGBMRegressor(n_estimators=1000, learning_rate=0.05, num_leaves=4,
subsample=0.6, colsample_bytree=0.4, reg_lambda=10, n_jobs=-1)
best_lgbm = print_best_params(lgbm_reg, lgbm_params)
LGBMRegressor 5 CV 시 최적 평균 RMSE 값: 0.1161, 최적 alpha:{'n_estimators': 1000}
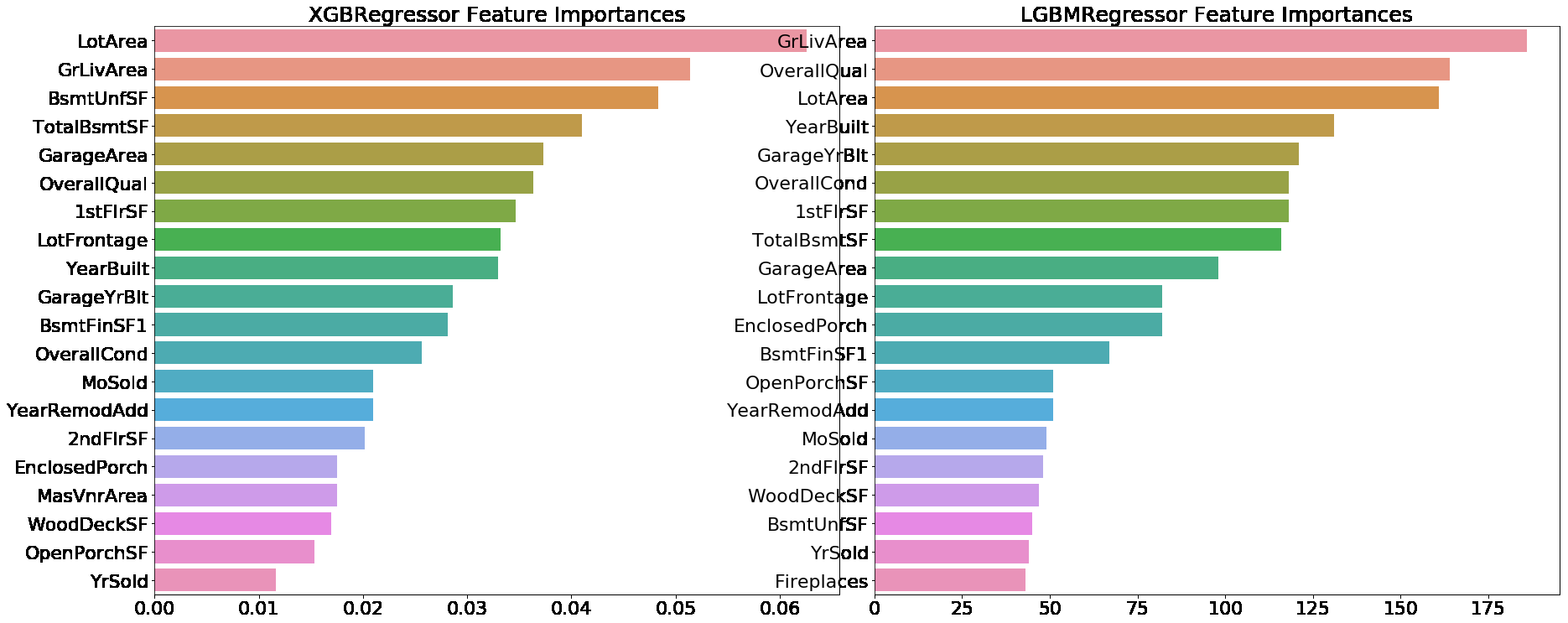
# 모델의 중요도 상위 20개의 피처명과 그때의 중요도값을 Series로 반환.
def get_top_features(model):
ftr_importances_values = model.feature_importances_
ftr_importances = pd.Series(ftr_importances_values, index=X_features.columns )
ftr_top20 = ftr_importances.sort_values(ascending=False)[:20]
return ftr_top20
def visualize_ftr_importances(models):
# 2개 회귀 모델의 시각화를 위해 2개의 컬럼을 가지는 subplot 생성
fig, axs = plt.subplots(figsize=(24,10),nrows=1, ncols=2)
fig.tight_layout()
# 입력인자로 받은 list객체인 models에서 차례로 model을 추출하여 피처 중요도 시각화.
for i_num, model in enumerate(models):
# 중요도 상위 20개의 피처명과 그때의 중요도값 추출
ftr_top20 = get_top_features(model)
axs[i_num].set_title(model.__class__.__name__+' Feature Importances', size=25)
#font 크기 조정.
for label in (axs[i_num].get_xticklabels() + axs[i_num].get_yticklabels()):
label.set_fontsize(22)
sns.barplot(x=ftr_top20.values, y=ftr_top20.index , ax=axs[i_num])
# 앞 예제에서 print_best_params( )가 반환한 GridSearchCV로 최적화된 모델의 피처 중요도 시각화
models = [best_xgb, best_lgbm]
visualize_ftr_importances(models)
회귀 모델들의 예측 결과 혼합을 통한 최종 예측
def get_rmse_pred(preds):
for key in preds.keys():
pred_value = preds[key]
mse = mean_squared_error(y_test , pred_value)
rmse = np.sqrt(mse)
print('{0} 모델의 RMSE: {1}'.format(key, rmse))
# 개별 모델의 학습
ridge_reg = Ridge(alpha=8)
ridge_reg.fit(X_train, y_train)
lasso_reg = Lasso(alpha=0.001)
lasso_reg.fit(X_train, y_train)
# 개별 모델 예측
ridge_pred = ridge_reg.predict(X_test)
lasso_pred = lasso_reg.predict(X_test)
# 개별 모델 예측값 혼합으로 최종 예측값 도출
pred = 0.4 * ridge_pred + 0.6 * lasso_pred
preds = {'최종 혼합': pred,
'Ridge': ridge_pred,
'Lasso': lasso_pred}
#최종 혼합 모델, 개별모델의 RMSE 값 출력
get_rmse_pred(preds)
최종 혼합 모델의 RMSE: 0.10007930884470517
Ridge 모델의 RMSE: 0.10345177546603249
Lasso 모델의 RMSE: 0.10024170460890039
xgb_reg = XGBRegressor(n_estimators=1000, learning_rate=0.05,
colsample_bytree=0.5, subsample=0.8)
lgbm_reg = LGBMRegressor(n_estimators=1000, learning_rate=0.05, num_leaves=4,
subsample=0.6, colsample_bytree=0.4, reg_lambda=10, n_jobs=-1)
xgb_reg.fit(X_train, y_train)
lgbm_reg.fit(X_train, y_train)
xgb_pred = xgb_reg.predict(X_test)
lgbm_pred = lgbm_reg.predict(X_test)
pred = 0.5 * xgb_pred + 0.5 * lgbm_pred
preds = {'최종 혼합': pred,
'XGBM': xgb_pred,
'LGBM': lgbm_pred}
get_rmse_pred(preds)
최종 혼합 모델의 RMSE: 0.10011146490791507
XGBM 모델의 RMSE: 0.10356482646891171
LGBM 모델의 RMSE: 0.1015065721553885
스태킹 모델을 통한 회귀 예측
from sklearn.model_selection import KFold
from sklearn.metrics import mean_absolute_error
# 개별 기반 모델에서 최종 메타 모델이 사용할 학습 및 테스트용 데이터를 생성하기 위한 함수.
def get_stacking_base_datasets(model, X_train_n, y_train_n, X_test_n, n_folds ):
# 지정된 n_folds값으로 KFold 생성.
kf = KFold(n_splits=n_folds, shuffle=False, random_state=0)
#추후에 메타 모델이 사용할 학습 데이터 반환을 위한 넘파이 배열 초기화
train_fold_pred = np.zeros((X_train_n.shape[0] ,1 ))
test_pred = np.zeros((X_test_n.shape[0],n_folds))
print(model.__class__.__name__ , ' model 시작 ')
for folder_counter , (train_index, valid_index) in enumerate(kf.split(X_train_n)):
#입력된 학습 데이터에서 기반 모델이 학습/예측할 폴드 데이터 셋 추출
print('\t 폴드 세트: ',folder_counter,' 시작 ')
X_tr = X_train_n[train_index]
y_tr = y_train_n[train_index]
X_te = X_train_n[valid_index]
#폴드 세트 내부에서 다시 만들어진 학습 데이터로 기반 모델의 학습 수행.
model.fit(X_tr , y_tr)
#폴드 세트 내부에서 다시 만들어진 검증 데이터로 기반 모델 예측 후 데이터 저장.
train_fold_pred[valid_index, :] = model.predict(X_te).reshape(-1,1)
#입력된 원본 테스트 데이터를 폴드 세트내 학습된 기반 모델에서 예측 후 데이터 저장.
test_pred[:, folder_counter] = model.predict(X_test_n)
# 폴드 세트 내에서 원본 테스트 데이터를 예측한 데이터를 평균하여 테스트 데이터로 생성
test_pred_mean = np.mean(test_pred, axis=1).reshape(-1,1)
#train_fold_pred는 최종 메타 모델이 사용하는 학습 데이터, test_pred_mean은 테스트 데이터
return train_fold_pred , test_pred_mean
# get_stacking_base_datasets( )은 넘파이 ndarray를 인자로 사용하므로 DataFrame을 넘파이로 변환.
X_train_n = X_train.values
X_test_n = X_test.values
y_train_n = y_train.values
# 각 개별 기반(Base)모델이 생성한 학습용/테스트용 데이터 반환.
ridge_train, ridge_test = get_stacking_base_datasets(ridge_reg, X_train_n, y_train_n, X_test_n, 5)
lasso_train, lasso_test = get_stacking_base_datasets(lasso_reg, X_train_n, y_train_n, X_test_n, 5)
xgb_train, xgb_test = get_stacking_base_datasets(xgb_reg, X_train_n, y_train_n, X_test_n, 5)
lgbm_train, lgbm_test = get_stacking_base_datasets(lgbm_reg, X_train_n, y_train_n, X_test_n, 5)
Ridge model 시작
폴드 세트: 0 시작
폴드 세트: 1 시작
폴드 세트: 2 시작
폴드 세트: 3 시작
폴드 세트: 4 시작
Lasso model 시작
폴드 세트: 0 시작
폴드 세트: 1 시작
폴드 세트: 2 시작
폴드 세트: 3 시작
폴드 세트: 4 시작
XGBRegressor model 시작
폴드 세트: 0 시작
폴드 세트: 1 시작
폴드 세트: 2 시작
폴드 세트: 3 시작
폴드 세트: 4 시작
LGBMRegressor model 시작
폴드 세트: 0 시작
폴드 세트: 1 시작
폴드 세트: 2 시작
폴드 세트: 3 시작
폴드 세트: 4 시작
# 개별 모델이 반환한 학습 및 테스트용 데이터 세트를 Stacking 형태로 결합.
Stack_final_X_train = np.concatenate((ridge_train, lasso_train,
xgb_train, lgbm_train), axis=1)
Stack_final_X_test = np.concatenate((ridge_test, lasso_test,
xgb_test, lgbm_test), axis=1)
# 최종 메타 모델은 라쏘 모델을 적용.
meta_model_lasso = Lasso(alpha=0.0005)
#기반 모델의 예측값을 기반으로 새롭게 만들어진 학습 및 테스트용 데이터로 예측하고 RMSE 측정.
meta_model_lasso.fit(Stack_final_X_train, y_train)
final = meta_model_lasso.predict(Stack_final_X_test)
mse = mean_squared_error(y_test , final)
rmse = np.sqrt(mse)
print('스태킹 회귀 모델의 최종 RMSE 값은:', rmse)
스태킹 회귀 모델의 최종 RMSE 값은: 0.09723804106266824
PREVIOUS경제