1463번 (1로 만들기)
- 내 풀이
N = int(input())
d = [0] * 1000001
# d = [0] * (N+1)
d[0] = 0
d[1] = 0
d[2] = 1
for i in range(3, N+1):
d[i] = d[i-1] + 1
if i % 3 == 0:
d[i] = min(d[i], d[i//3] + 1)
if i % 2 == 0:
d[i] = min(d[i], d[i//2] + 1)
print(d[N])
변수를 입력받은 후 그에 걸맞게 메모리를 할당하는 방식인 동적할당을 사용하려 했으나 index error가 발생하였다. 그 원인은 N=0 일 때 d[2]에 접근할 수 없어서 생기는 에러였다. DP 테이블을 초기화 할 때는 항상 동적할당이 아닌 정적할당으로 초기화 해주는 게 좋을 듯 하다.
11727번 (2xn 타일링 2)
- DP 문제이기는 하지만 완전 탐색과 DFS 등의 개념을 보고 있었어서 먼저 DFS로 풀어보고자 하였다.
- 테스트 케이스의 경우는 맞췄지만 제출하니 run time error가 발생하였다.
import sys
sys.setrecursionlimit(10000)
N = int(input())
answer = 0
# 중복 허용 및 순서 고려하는 순열
def dfs(depth):
global answer
if depth == N: # 다 채웠으면 경우의 수 1개 채워
answer += 1
return
for i in range(3):
# 마지막 한 칸 넣는건데 가로 두칸짜리 블록 넣는거 피하기 위함
if i >= 1 and depth == N-1:
continue
if i == 0:
dfs(depth+1) # 세로 한칸은 한칸 채우는 것
if i == 1:
dfs(depth+2) # 세로 두칸은 두칸 채우는 것
if i == 2:
dfs(depth+2) # 다른 유형의 2칸 채우는 것
dfs(0)
print(answer % 10007)
2293번 (동전 1)
4줄짜리 코드 이해하는데 5시간 걸린 문제다… ㅜㅜ
핵심은 아래와 같다.
d[i]: 모든 동전 종류를 중복을 허용하며 뽑았을 때의 합이i원인 경우의 수- 로직 이해하기
- 먼저 이해를 돕기 위해, 이 로직은
coins = [1, 2, 5] \n for c in coins:를 통해 동전을 하나씩 선택하고, 그 동전으로 만들 수 있는 경우의 수를 기존에 선택한 동전이 만들어낸 경우의 수를 누적해서 더하는 방식으로 구현되어 있다는 것을 숙지하자. - 가장 처음, 동전 1원이 선택되었을 경우
d[1] = d[1] + d[0],d[1] = d[2] + d[1], … ,d[10] = d[10] + d[9]를 의미하는d[i] = d[i] + d[i-1]의 우변 항이 의미하는 바는 다음과 같다.d[i-1]: 여태까지 구한 각 경우에 대해 맨 끝에 1만 붙여준 것d[i]: 여태까지 구한 경우 누적을 위해 존재 (메모이제이션 기능 수행을 위한 항)- 현재는 동전 1원에 대해서만 시행한 것이므로 아직 이해가 안될 것이다. 2원짜리 동전이 활용되는 다음 부분을 보자
for c in coins의 두번째 c 값으로 2원이 뽑힌 경우. (메모이제이션으로 인해 1원, 2원이 모두 활용되는 경우가 계산됨)d[i] = d[i-2] + d[i]1원만 있을 경우에 비해 이번에는 2가지 종류의 동전이 있고, 이때는d[i]에다가(현재의d[i]는 이미 1원만 선택했을때 계산된 경우의 수가 들어가있음) +d[i-2](이미 d[i-2]도 이전에 1원짜리로만 할 수 있는 경우의 수 값이 들어있는 상태)의 모든 경우 맨 끝에 2를 세운 경우의 수가 같이 더해지기 때문에d[i]는 1원, 2원을 모두 활용했을 때 나오는 경우의 수가 된다.- 즉 여태까지 한 내용을 요약하면, i원을 만들기 위해 1원, 2원으로 할 수 있는 모든 경우의 수를 구한 것이다. 다음의
for c in coins경우를 통해 5원짜리 동전에 대해서 같은 내용을 수행하면, i원을 만들기 위해 1, 2, 5원짜리 동전이 모두 활용된 경우의 수가dp[i]에 저장된다.
- 먼저 이해를 돕기 위해, 이 로직은
for c in coins: # c는 coin 종류
for i in arr: # dp 테이블 채우기 위한 for문
if i-coin >= 0: # Index Error 방지
d[i] += d[i-c]
이때 중요한것이 d[0] = 1로 초기화 하는 것이다. 그 이유는 동전 종류가 1이 있다고 생각해 봤을 때 d[1] = d[0] + d[1]로 d[1] = 1로 만들기 위해선 d[0] = 1이 되어야 하기 때문이다. 동전 종류가 2원일 때 d[2] = d[2] + d[0]에서의 d[0]이 0을 만드는 경우의 수에 맨끝에 2를 붙이는 경우의 수 이므로 1이 된다. 이 말을 받아들이기는 처음엔 좀 당황스러울 것이나, 계속 생각하고 직접 종이에 써가면서 보면 그 흐름이 이해가 갈 것이다.
위 코드 흐름을 보고 다시 다이나믹 프로그래밍 개념에 대해서 복기해보자. 다이나믹 프로그래밍은 2가지를 기억해야 한다.
- 전체 문제를 부분 문제로 쪼갤 수 있다.
- 이전에 구한 부분 문제의 값을 현재 문제에 재사용 할 수 있다.
이 2가지를 기억하면서 위 Logic을 2293번 문제를 다시 정리해보자.
- 전체 문제를 부분 문제로 쪼갤 수 있다.
- 모든 동전을 활용했을 때 값이 K가 나오도록 하는 조합의 수 -> 모든 동전을 활용했을 때 값이 1<= i <= K 가 나오도록 하는 조합의 수 -> 모든 동전을 활용했을 때 값이 i 가 나오도록 하는 조합의 수
- 이전에 구한 부분 문제의 값을 현재 문제에 재사용 할 수 있다.
for coins = [1, 2, 5] \n for c in coins:를 예로 들어서, 특정 동전(1원일 때, 2원일 때, 5원일 때)에 대해서 경우의 수를 구하는데, 5원에 대해 경우의 수를 구하는 상황에는 이미 1, 2원을 활용한 경우의 수가dp테이블에 저장되어 있는 상태. 즉 기존 부분문제 값을 현재 문제에 재사용 하는 것이 된다.
다음은 정답 코드이다.
import sys
N, K = map(int, sys.stdin.readline().rstrip().split())
coins = []
for i in range(N):
coins.append(int(sys.stdin.readline().rstrip()))
coins.sort() # 꼭 sort 할 필요는 없다.
d = [0] * 10001
d[0] = 1
for c in coins:
for i in range(c, K+1):
if i - c >= 0:
d[i] = d[i] + d[i-c]
print(d[K])
2294 (동전 2)
출처: 백준
난이도: 골드4
- 한방에 맞췄당
import sys
N, M = map(int, sys.stdin.readline().rstrip().split())
arr = []
for _ in range(N):
arr.append(int(input()))
d = [1e9] * 100001
d[0] = 0
for i in range(1, M+1):
for j in arr:
if 0<= i-j < M+1:
d[i] = min(d[i], d[i-j] + 1)
if d[M] == 1e9:
print(-1)
else:
print(d[M])
2193번 (이친수)
처음에 못풀고 나중에 다시 풀었을 때, 향상된 추상화 실력으로 피보나치 수열임을 간파하여 풀기는 하였으나, DP 방식을 이용해 풀지 못해서 찜찜했다. DP 방식을 꾸역꾸역 적용해서 풀어보려고 했는데 아래와 같이 잘못 접근 했다. 잘못 접근한 방식을 보고, 다음부턴 이렇게 하지 말자.

초기 접근 방식. 뭔가 점화식을 도출 할 수 있을듯한 느낌이 들었다.
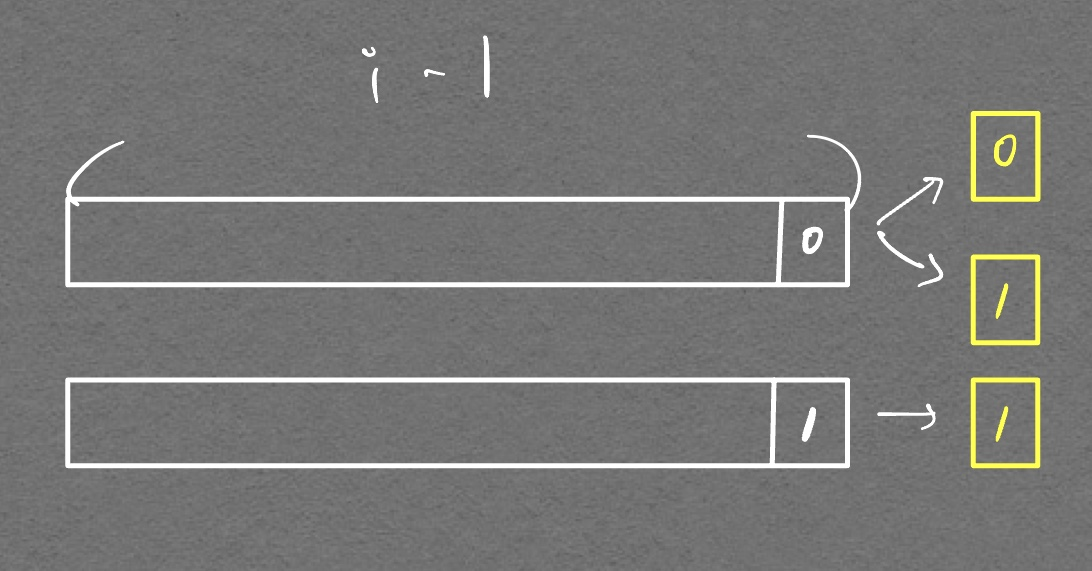
그러나 \(dp[i] = something\) 으로 점화식을 세우려면, dp[i-1]의 경우의 수가 각각 맨 끝이 0인것, 1인것으로 나눠줘야 하는 추가 조건이 붙는다. DFS 형태로 구현하면서 맨 뒤에 11이 연속으로 붙는경우를 제외한다면, 문제를 풀 수 있겠지만 \(O(2^{90})\) 이라는 괘랄한 시간복잡도가 발생하기에 (DFS 90번 연속 호출로 인해 for문이 90번 중복된다) 시간초과가 발생한다. 고로 깔끔하게 점화식을 설계하고, 메모이제이션을 해서 \(O(n^3)\) (n이 약 \(10^2\)라고 가정했을 때) 안에 풀어내야 한다.
즉, \(dp[i] = something\) 으로 깔끔하게 점화식을 세울 수 없다.
그렇다면 어떻게 해야 깔끔하게 점화식을 세울 수 있을까? 아래와 같이 생각하면 가능하다.
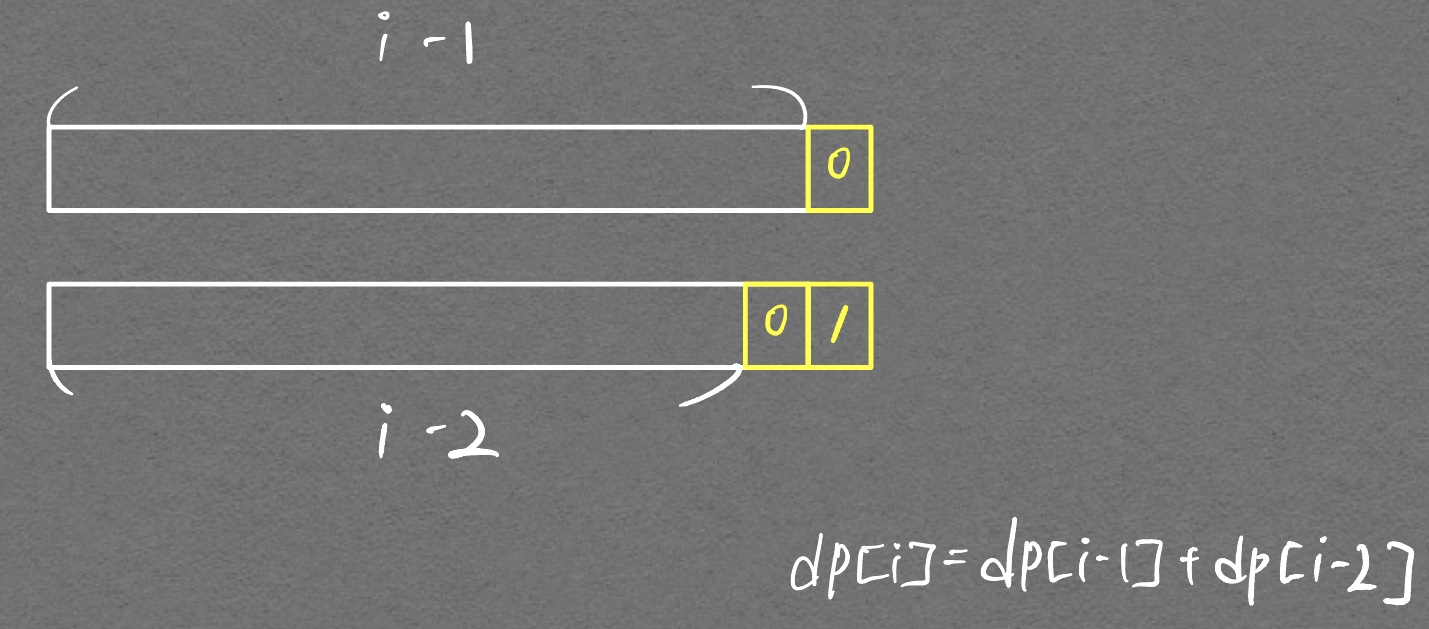
dp[i]는 2가지 경우로 나뉠 수 있다. 가장 끝에 0이 오는것과, 가장 끝에 1이 오는 것으로. 그럼 이걸 어떻게 깔끔하게 점화식을 세울 수 있을 까? 위와 같이 가장 끝에 0은 이전의 모든 경우에 붙일 수 있단 것을 적극 활용한다. 이걸로 점화식이 세워진다. 가히 예술이다…
import sys
N = int(sys.stdin.readline().rstrip())
explorer = [1]
cnt = 0
def dp():
d = [0] * 91
d[0] = 0
d[1] = 1
d[2] = 1
for i in range(3, N+1):
d[i] = d[i-2] + d[i-1]
print(d[N])
dp()
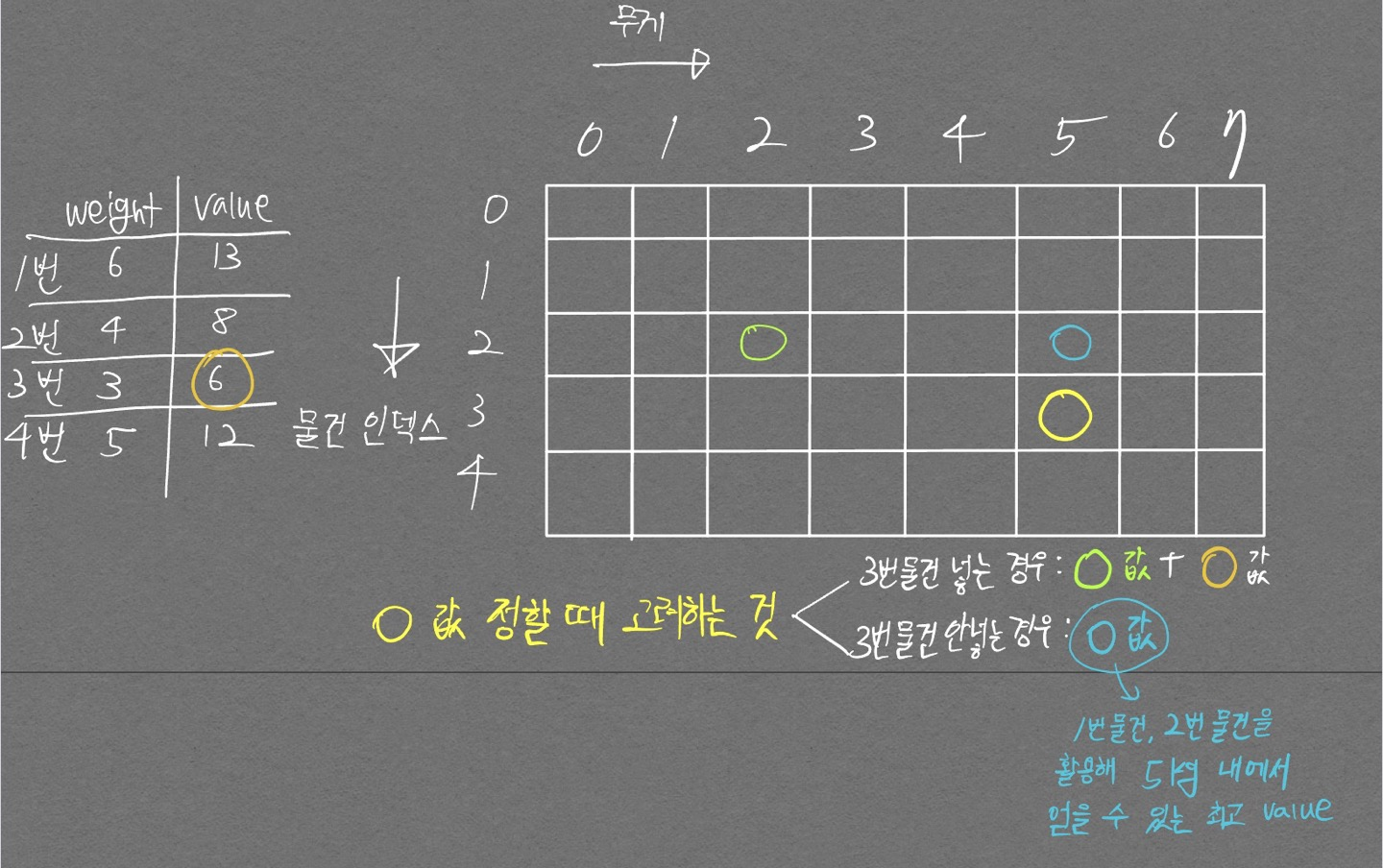
12865번 (평범한 배낭) - 다시 풀어볼 것. 2022.10.18
- DP가 좀 익숙해지니 table을 2차원으로 구성해야 한다는것 까지는 알았음. 풀진 못했지만 ㅋㅋ
- 핵심 그림
2533번 (사회망 서비스)
- 다시 풀어야 하는 문제다. 아주 어렵다 ㅜㅜ
- DFS 개념, DP 개념이 들어가고 마지막 답을
print(min(dp[N][0], dp[N][1]))로 하면 에러가 난다. N 대신 N-1을 넣으면 통과가 된다. 대체 뭔 차이지..
import sys
sys.setrecursionlimit(int(1e9))
N = int(sys.stdin.readline().rstrip())
# 무방향 그래프.
# 인접 그래프 형태로 구현
# 1부터 Node가 시작하는것을 고려해줌
'''
N이 10^6 이므로 인접리스트로 구현하면 망함..
10^12면 메모리 부움..
'''
# graph = [[INF] * (N+1) for _ in range(N+1)]
graph = [[] for _ in range(N+1)]
for _ in range(N-1):
a, b = map(int, sys.stdin.readline().rstrip().split())
graph[a].append(b)
graph[b].append(a)
# graph[a][b] = 1
# graph[b][a] = 1
# print(graph)
# print(graph[3])
dp = [[0, 1] for _ in range(N+1)]
visit = [False] * (N+1)
# Tree의 leaf Node와 DP를 섞는 개념
# leaf Node 까지 방문
# 근데 방문조건을 꼭 설정해줘야 하는디..
def dfs_dp(node):
# 방문 처리
visit[node] = True
# Node에서 출발하는 모든 Node들의 연결정보
# for idx, connected in enumerate(graph[node]):
for child in graph[node]:
# 종료조건은 더이상 들어갈 Node가 없을 때
# if connected==1 and not visit[idx]:
if not visit[child]:
# if child == 1 and not visit[child]:
dfs_dp(child)
# 현재 노드가 얼리어답터라면
# 자식 노드들은 얼리든 아니든 상관없음
dp[node][0] += dp[child][1]
# 현재 노드가 얼리어답터가 아니라면
# 연결된 자식들은 모두 얼리어답터여야 함
dp[node][1] += min(dp[child][0], dp[child][1])
dfs_dp(N-1)
# print(dp)
# 뭐든 상관 없는듯..?
print(min(dp[N-1][0], dp[N-1][1]))
카카오 2022년 하반기 신입 공채 2번(아마도 DP 문제였던것으로 기억)
.