1756번 (피자 굽기)
뒤에서부터 인덱싱 하는 방식으로 O(N)만에 풀기
처음 접근했을 땐 완탐으로 밖에 생각나지 않아서 시간초과로 문제를 풀지 못했다. O(N*M)을 O(M)으로 줄이기 위해 다음의 2가지가 제일 중요했다.
-
어차피 나중에 더 지름이 넓더라도 중간에 피자가 걸리면 무쓸모기 때문에 피자 오븐의 지름을 다음으로 여길 수 있다.
5 6 4 3 6 2 3->5 5 4 3 3 2 2 -
피자를 놓을 수 있는건 맨 뒤에서부터 차례대로 가능한지를 보는 로직으로 구성한다. 이를 통해 피자별로 다시 처음부터 탐색할 필요가 없다.
- 처음 답안 맞춘 코드
d, m = map(int, input().split())
depths = list(map(int, input().split()))
visit = [False for _ in range(len(depths))]
pizzas = list(map(int, input().split()))
# 피자 depth 스케일링
for idx, i in enumerate(depths):
# 끝부분에서는 그냥 종료
if idx+1 >= len(depths):
break
if depths[idx+1] > depths[idx]:
depths[idx+1] = depths[idx]
# 제일 끝 부분부터 체크
# deque로 popleft() 사용
from collections import deque
q = deque(pizzas)
answer = len(depths) - 1
for idx, i in enumerate(depths[::-1]): # 뒤에서 부터 O(D) 시간복잡도로 처리
# q가 비지 않고 넣을 수 있다면
if q and i >= q[0]:
q.popleft()
# q가 비었다면
if not q:
break
answer -= 1
# 나는 for문은 깊이가 0부터 시작되는걸로 생각하고 구현했기에, 막판에 +1 해줘야함
print(answer + 1)
위 방식은 내가 초기에 짠 코드인데, for문에서의 종료조건이 가장 위에 있지 않은 것 부터 마음에 들지 않는다. 종료 조건이 뒷 부분에 있기 때문에 문제가 더 복잡해질 경우, 엣지 케이스를 발견하기 힘들 것으로 보인다. 따라서 다음과 같이 직관성을 살려봤다.
d, m = map(int, input().split())
depths = list(map(int, input().split()))
visit = [False for _ in range(len(depths))]
pizzas = list(map(int, input().split()))
# 피자 depth 스케일링
for idx, i in enumerate(depths):
# 끝부분에서는 그냥 종료
if idx+1 >= len(depths):
break
if depths[idx+1] > depths[idx]:
depths[idx+1] = depths[idx]
# 제일 끝 부분부터 체크
# deque로 popleft() 사용
from collections import deque
q = deque(pizzas)
# answer = len(depths) - 1
answer = -1
for idx, i in enumerate(depths[::-1]): # 뒤에서 부터 O(D) 시간복잡도로 처리
# q가 비었다면
# 더이상 찾을게 없으니 break
if not q:
break # 그러나 생각해봐야 할 것은 현재 보고 있는 answer(마지막 깊이 값)은
# 여기 바로 이전 값으로 쳐야함
# 현재 answer은 지금 보고 있는 위치값을 가지고 있음
# 현재 위치를 넣을 수 있다면. 현재 위치로 answer를 갱신
if q and i >= q[0]:
q.popleft()
answer = len(depths)-1 - idx # 이런식으로 idx를 활용해서 현재 depth값을 찾는게 좋을 듯
# q가 비지 않았다면
if q:
print(0)
else:
print(answer + 1)
현재 위치에 피자를 삽입할 수 있을 경우에만! answer 값을 갱신해주는 로직으로 변경하니, 종료조건도 for문의 가장 초기에 넣을 수 있어서 전체적인 코드 흐름이 훨씬 이해가 잘 갔다. 이런식으로 바로 짤 수 있도록 연습하자.
이진탐색 방식으로 O(NlogN)만에 풀기
갑자기 cpp로 풀고싶어서 cpp로 해따..
#include<iostream>
#include<vector>
using namespace std;
int max_depth;
int binary_search(vector<int> &depths, int key) {
int start = 0;
//int end = depths.size() - 1;
int end = max_depth;
int pos = 0;
while (start <= end) {
int mid = (start + end) / 2;
if (depths[mid] >= key) {
pos = mid;
start = mid + 1;
}
else {
end = mid - 1;
pos = mid - 1;
}
}
max_depth = pos-1;
return pos;
}
int main() {
int D, N;
vector<int> depths;
cin >> D >> N;
for (int i = 0; i < D; i++) {
int depth;
cin >> depth;
depths.push_back(depth);
}
// O(n)으로 깊이 바꾸기
for (int i = 1; i < D; i++) {
if (depths[i] > depths[i - 1]) {
depths[i] = depths[i - 1];
}
}
max_depth = depths.size() - 1;
// 이진 탐색
int answer = 0;
for (int i = 0; i < N; i++) {
int key;
cin >> key;
answer = binary_search(depths, key);
if (i == N - 1) {
if (answer != 0) cout << answer + 1;
else cout << answer;
}
}
return 0;
}
처음에 난 이분 탐색으로 왜 접근이 가능한지 이해하지 못했다. 왜냐하면
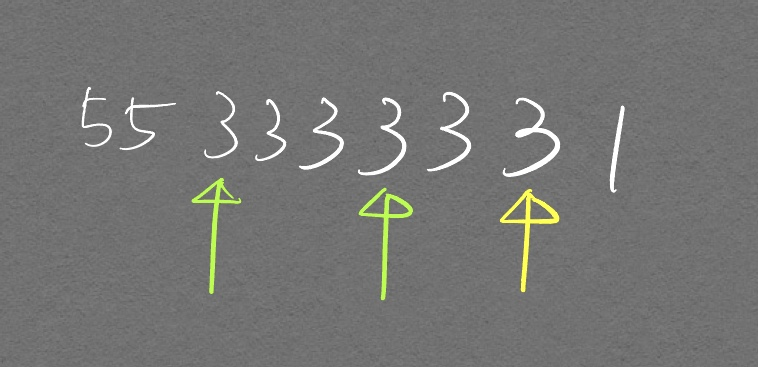
이진 탐색으로 어떻게 노란색 부분에 피자를 넣을 수 있을까?
자칫 잘못하면 초록색 화살표 같은곳에 피자가 들어가는 경우도 생기는 것 아닌가?
라고 생각했기 때문이다.
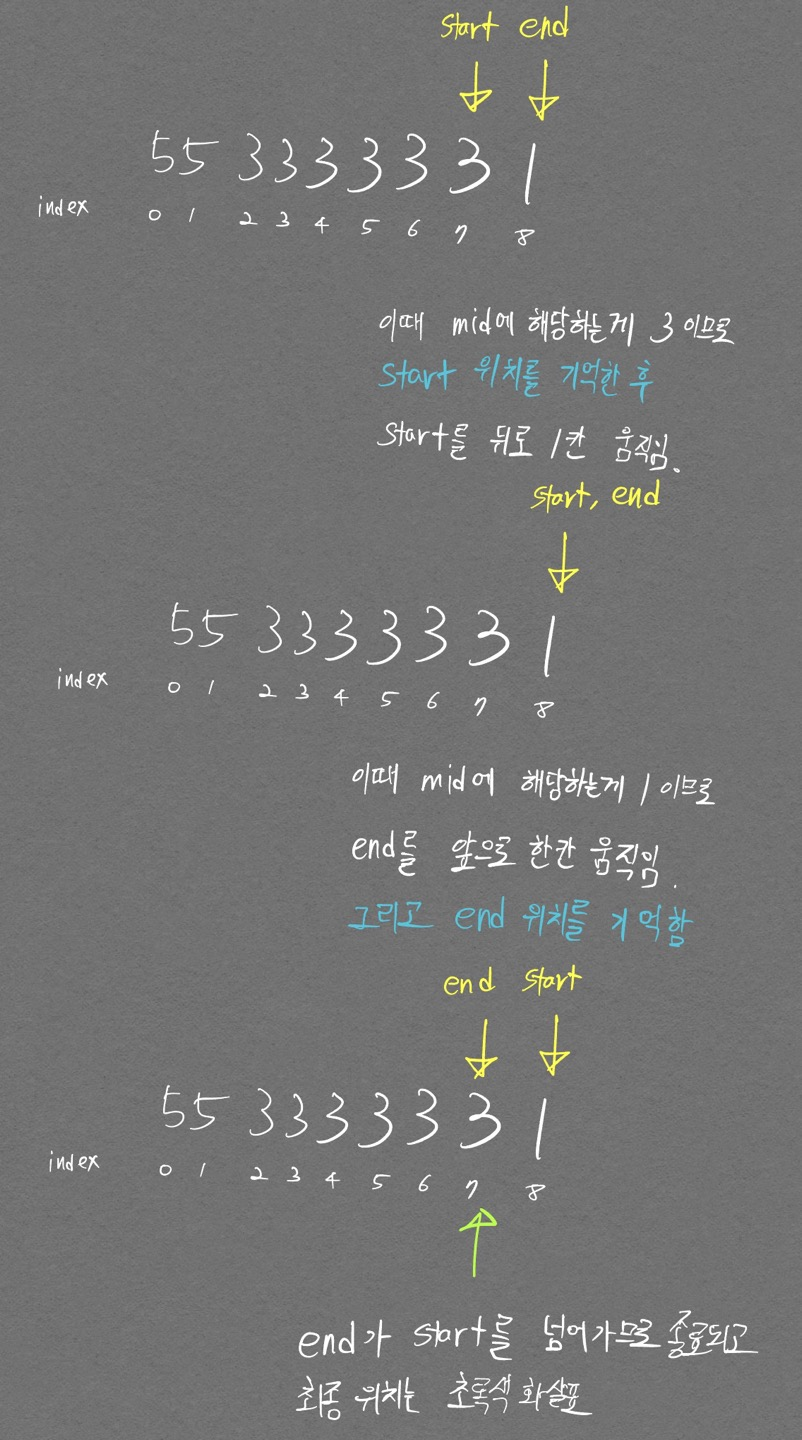
그 의문은 다음의 2가지로 풀리게 된다.
- 3을 찾았다고 해서 이진 탐색을 종료시키지 않는다.
- 종료 시점에서 위치를 기억할 코드를 2가지 경우로 나눈다.
- start 인덱스가 바뀔 때
- end 인덱스가 바뀔 때
아래 그림을 천천히 따라가면 이해가 갈 것이다.
간혹가다가 start, end 포지션이 아래와 같이 지정이 된다면 문제가 안 풀리지 않을까?

정답은 위와 같이 start, end가 저렇게 배정될 일이 없다는 것이다. 이진 탐색 함수가 실행될 때 start, end는 가능한 구역의 처음과 끝 인덱스로 각각 초기화 된다.
그 이후 mid인덱스의 크기를 보고 start가 움직이거나 end가 움직이게 되는데 위와 같은 경우가 발생하려면 동일한 mid 값에 대해 어쩔땐 start에서 움직이고, 어쩔땐 end에서 움직여야한다. 이는 이진 탐색 알고리즘에서 발생할 수 없는 경우니 배제해도 된다.