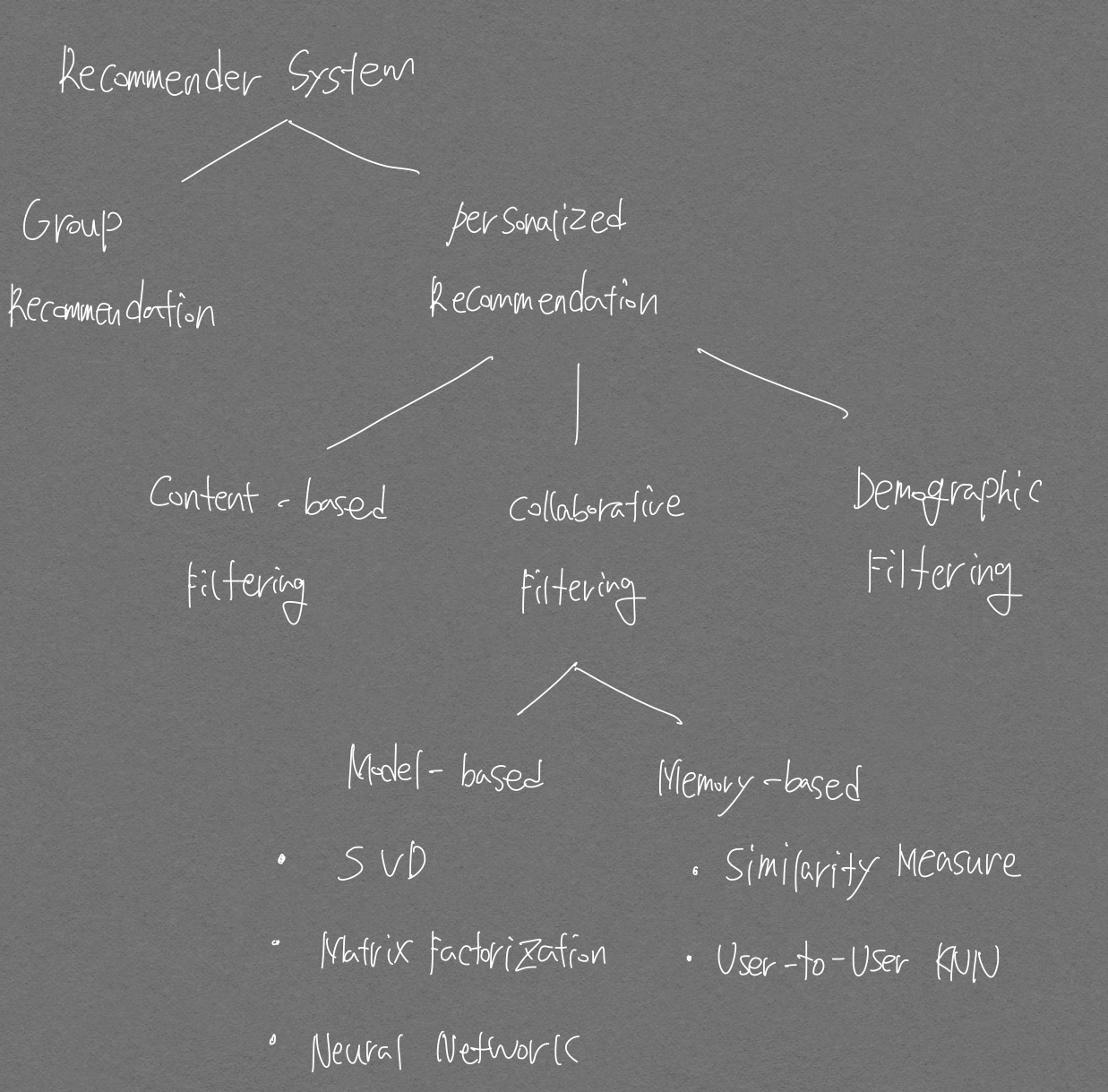
구조도
추천시스템 수업 강의자료
파이썬 머신러닝 완벽가이드 구조도.
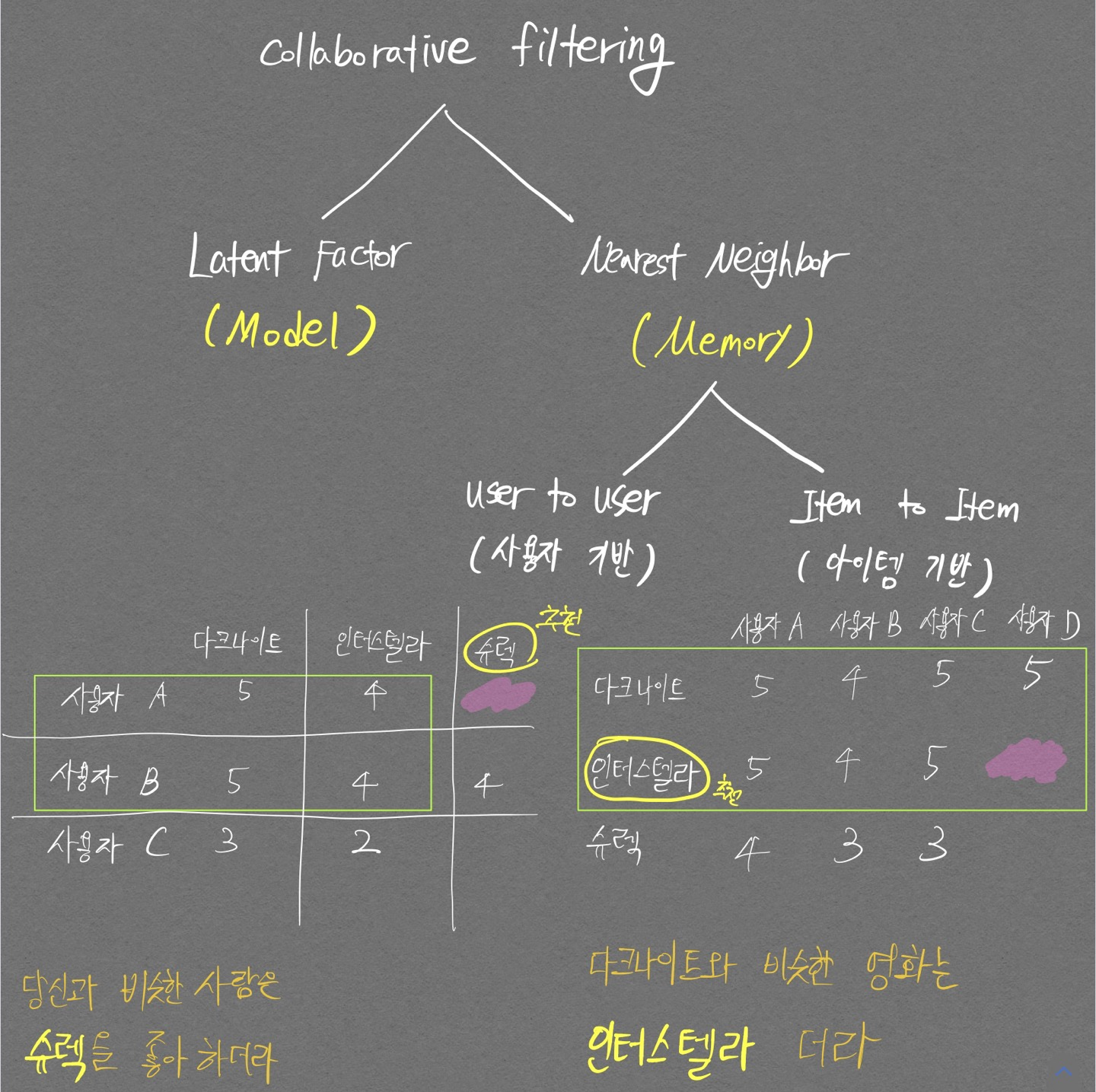
아래 행렬표의 왼쪽 그림이 사용자 기반, 오른쪽 그림이 아이템 기반
Content-based filtering
콘텐츠 기반 필터링이다. 추천하고자 하는 아이템이 영화라고 했을 때 콘텐츠는 장르, 평점, 등장인물등 영화를 구성하는 속성값 으로 볼 수 있을듯 하다.
코드 구현
Collaborative filtering
가장 많이 사용되는 추천시스템 기법으로, 사용자가 아이템을 매긴 평점 정보나 상품 구매 이력과 같은 사용자 행동 양식(User Behavior)만을 기반으로 추천하는 것이다.
Collaborative filtering은 다음의 두가지로 나뉘게 되며 각 항목별로 설명하고자 한다.
- Nearest neighborhood: 유저 기반, 아이템 기반으로 다시 나뉜다.
콘텐츠 기반 필터링과아이템 기반 협업 필터링의 차이점: 영화를 예시로 들 때, 내 생각에콘텐츠 기반 필터링은 콘텐츠들을 활용해 영화간의 similarity를 구해 사용자에게 영화를 추천해주는 것이고,아이템 기반 협업 필터링은 User의 영화 평가 정보(User behavior)를 활용해 영화간의 similarity를 구해 사용자에게 영화를 추천해주는 것인듯 하다. 추가적으로유저 기반 협업 필터링은 User의 영화 평가 정보를 활용해 유저간의 similarity를 구해 사용자에게 영화를 추천해주는 듯 하다.
- Latent factor
Nearest neighborhood
2가지 방식인 Item-Based, User-Based으로 나뉜다.
Item-Based
코드 구현
MovieLens 아이템 기반 협업 필터링 추천 시스템 포스트
User-Based
Latent Factor
행렬 분해(Matrix Factorization)을 활용해 Collaborative filtering을 구현하는 것을 의미한다.
user-item score matrix 가 있을 때 행렬 분해를 적용하면 비어있는 값들을 채운 predicted score matrix 를 만들 수 있게 된다.
주목할 만한 점은 이때의 user-item score matrix는 대부분의 값이 비워져있는 sparse matrix 이다.
행렬 분해를 적용하기 위해 SVD(Singular Vector Decomposition) 방법을 자주 사용하지만 sparse matrix에 대해서 SVD를 바로 적용할 수 없어서 확률적 경사 하강법(Stochastic Gradient Descent)이나 ALS(Alternating Least Squares) 방식을 이용해 SVD를 수행한다.
코드 구현
MovieLens 행렬 분해 잠재요인 협업 필터링 추천 시스템 포스트
확률적 경사 하강법 적용 SVD
import numpy as np
# 원본 행렬 R 생성
# 분해 행렬 P, Q 초기화
# 잠재 요인 차원 K는 3으로 설정
R = np.array([[4, np.NaN, np.NaN, 2, np.NaN],
[np.NaN, 5, np.NaN, 3, 1],
[np.NaN, np.NaN, 3, 4, 4],
[5, 2, 1, 2, np.NaN]])
num_users, num_items = R.shape
K=3
# P와 Q 행렬의 크기를 지정하고 정규 분포를 가진 임의의 값으로 입력
np.random.seed(1)
# np.random.normal 함수는 정규분포를 띄며 scale은 표준편차를 의미함.
P = np.random.normal(scale=1./K, size=(num_users, K))
Q = np.random.normal(scale=1./K, size=(num_items, K))
print(P)
print(Q)
[[ 0.54144845 -0.2039188 -0.17605725]
[-0.35765621 0.28846921 -0.76717957]
[ 0.58160392 -0.25373563 0.10634637]
[-0.08312346 0.48736931 -0.68671357]]
[[-0.1074724 -0.12801812 0.37792315]
[-0.36663042 -0.05747607 -0.29261947]
[ 0.01407125 0.19427174 -0.36687306]
[ 0.38157457 0.30053024 0.16749811]
[ 0.30028532 -0.22790929 -0.04096341]]
arr = np.array([[1,2,3],[4,5,6]])
print(f"arr: \n{arr} \n")
print(f"arr[[0, 1], [1,2]]: \n{arr[[0,1 ], [1,2]]}")
arr:
[[1 2 3]
[4 5 6]]
arr[[0, 1], [1,2]]:
[2 6]
from sklearn.metrics import mean_squared_error
def get_rmse(R, P, Q, non_zeros):
error = 0
# 두 개의 분해된 행렬 P와 Q.T의 내적으로 예측 R 행렬 생성
full_pred_matrix = np.dot(P, Q.T)
# 실제 R 행렬에서 널이 아닌 값의 위치 인덱스 추출해 실제 R 행렬과 예측 행렬의 RMSE 추출
x_non_zero_ind = [non_zero[0] for non_zero in non_zeros]
y_non_zero_ind = [non_zero[1] for non_zero in non_zeros]
R_non_zeros = R[x_non_zero_ind, y_non_zero_ind]
full_pred_matrix_non_zeros = full_pred_matrix[x_non_zero_ind, y_non_zero_ind] # 이런식으로 x좌표를 row 자리에, y좌표를 column 자리에 배치하여 여러 값들에 인덱싱이 가능하다
mse = mean_squared_error(R_non_zeros, full_pred_matrix_non_zeros)
rmse = np.sqrt(mse)
return rmse
# R > 0인 행 위치, 열 위치, 값을 non_zeros 리스트에 저장
non_zeros = [(i, j, R[i, j])for i in range(num_users) for j in range(num_items) if R[i, j] > 0]
steps = 1000
learning_rate = 0.01
r_lambda = 0.01
# SGD 기법으로 P, Q 매트릭스 계속 업데이트.
for step in range(steps):
for i, j, r in non_zeros:
# 실제 값과 예측 값의 차이인 오류 값 구함
# P, Q 행렬은 정규분포로 초기화 해둔 상태여서 Null값이 없음
eij = r - np.dot(P[i, :], Q[j, :].T) # Q에 대해 전치를 하기때문에 j 변수가 row 인덱스 쪽으로 온다
# Regularization을 반영한 SGD 업데이트 공식 적용
P[i, :] = P[i, :] + learning_rate * (eij * Q[j, :] - r_lambda * P[i, :])
Q[j, :] = Q[j, :] + learning_rate * (eij * P[i, :] - r_lambda * Q[j, :])
rmse = get_rmse(R, P, Q, non_zeros)
if (step%50) == 0:
print("### Iteration step: ", step, "rmse: ", rmse)
### Iteration step: 0 rmse: 3.261355059488935
### Iteration step: 0 rmse: 3.26040057174686
### Iteration step: 0 rmse: 3.253984404542389
### Iteration step: 0 rmse: 3.2521583839863624
### Iteration step: 0 rmse: 3.252335303789125
### Iteration step: 0 rmse: 3.251072196430487
### Iteration step: 0 rmse: 3.2492449982564864
### Iteration step: 0 rmse: 3.247416477570409
### Iteration step: 0 rmse: 3.241926055455223
### Iteration step: 0 rmse: 3.2400454107613084
### Iteration step: 0 rmse: 3.240166740749792
### Iteration step: 0 rmse: 3.2388050277987723
### Iteration step: 50 rmse: 0.5003190892212748
### Iteration step: 50 rmse: 0.5001616291326989
### Iteration step: 50 rmse: 0.49899601202578087
...
### Iteration step: 950 rmse: 0.015972009545965248
### Iteration step: 950 rmse: 0.0161070634587959
### Iteration step: 950 rmse: 0.016192355609214733
### Iteration step: 950 rmse: 0.016447171683479155
# P, Q.T 내적 결과 확인.
print(np.dot(P, Q.T))
[[3.99127879 1.38011248 1.22717318 1.99969301 1.63600009]
[5.90537068 4.97742516 0.85959715 2.98397607 1.00334834]
[6.15298189 1.22747711 2.9872171 3.97842077 3.98565348]
[4.97037862 2.00475587 1.00592323 2.00945909 1.34879089]]
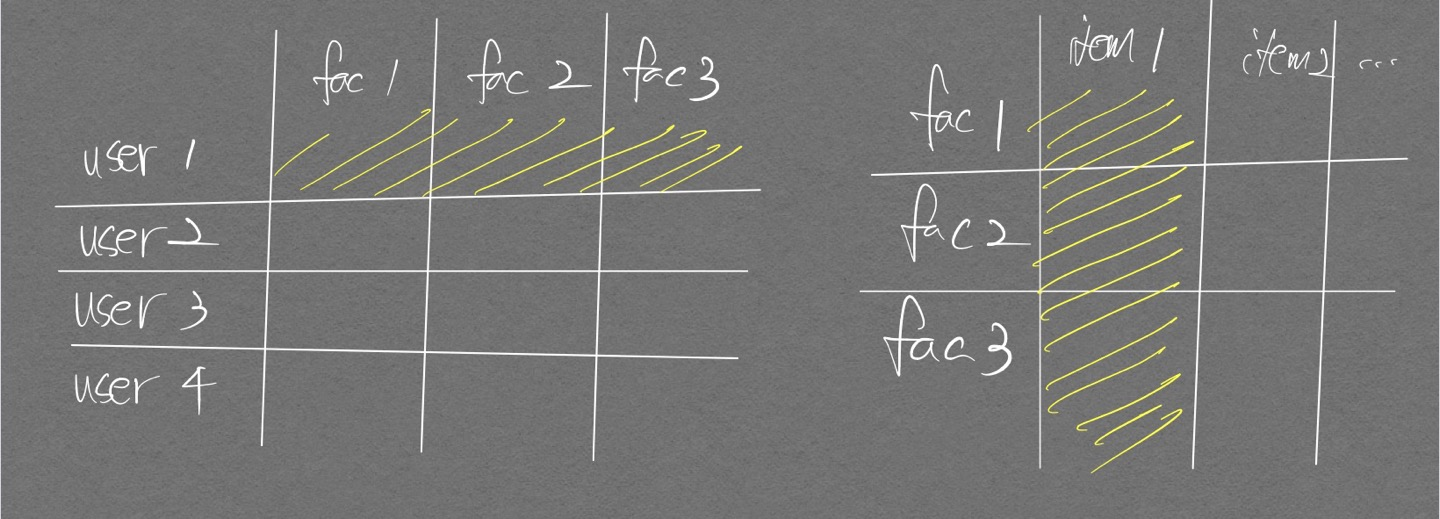
전치 행렬 생각할 때는 먼저 인덱싱 부분을 표시한 후 전치를 생각하면 편하다.
아래 그림 오른쪽 행렬(Q 행렬) 참고.
Memory based 방식
Similarity를 이용함.
Model based 방식
SVD, KNN과 같이 이미 구현되어있는 Model 이용함.