벡터

벡터를 생각할 땐 화살표를 떠올리자

• 그 화살표는 항상 원점에 있음(선형대수학적 관점으로 보려면 원점에 놓여있다고 생각해야 편하다고함)

스칼라

• 벡터를 스케일하는 숫자
  • 스케일이란 벡터의 방향은 유지한채(음수를 곱하면 방향이 뒤집힘) 길이를 늘리고 줄이고 하는 것

벡터방정식

• 방정식이란?
  • 미지수를 포함하는 등식에서, 그 미지수에 특정한 수치를 넣었을 때만 성립하는 것
• 벡터방정식이란?
  • 위 방정식의 개념의 미지수가 벡터
  • 원점에서 시작되는 벡터들의 조합으로 직선, 평면등을 표현해냄
  • 장점
    • 3차원, 4차원으로의 확장이 매우 용이함

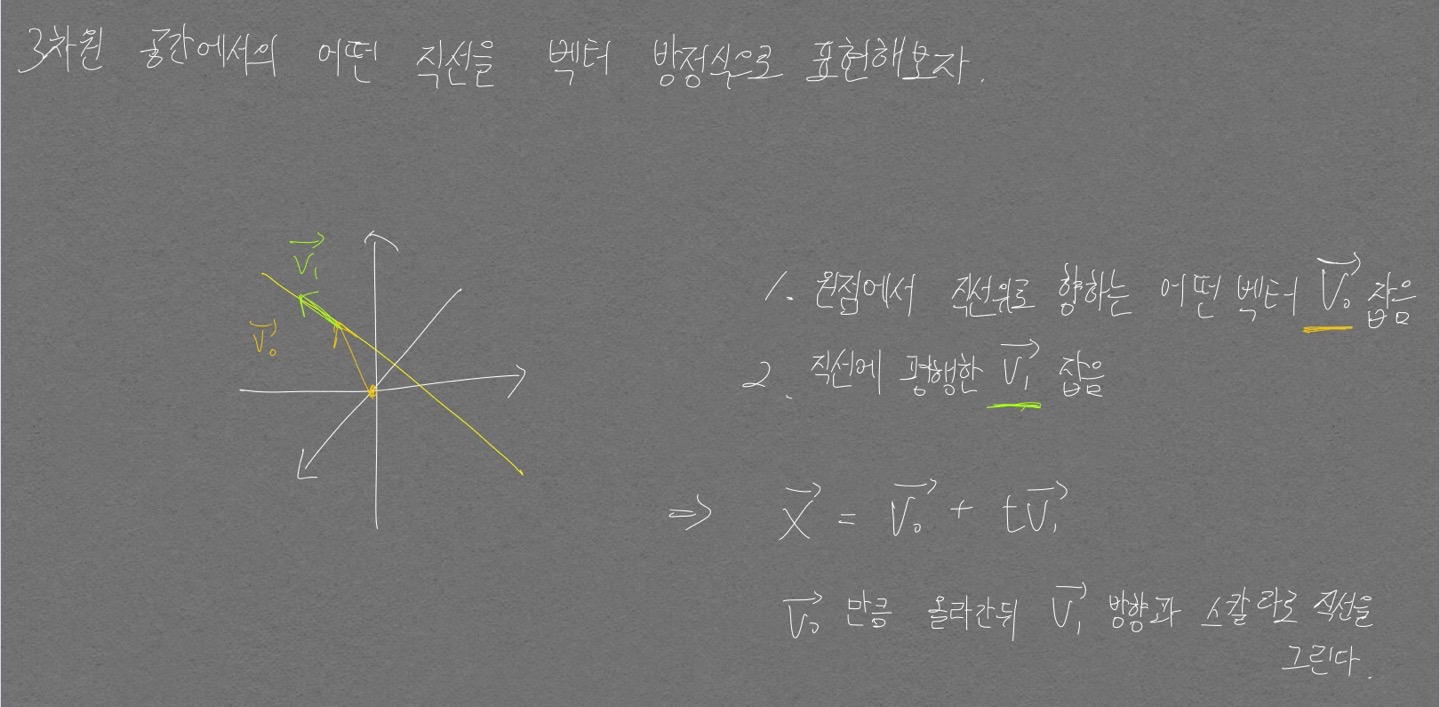
  • 직선의 벡터방정식

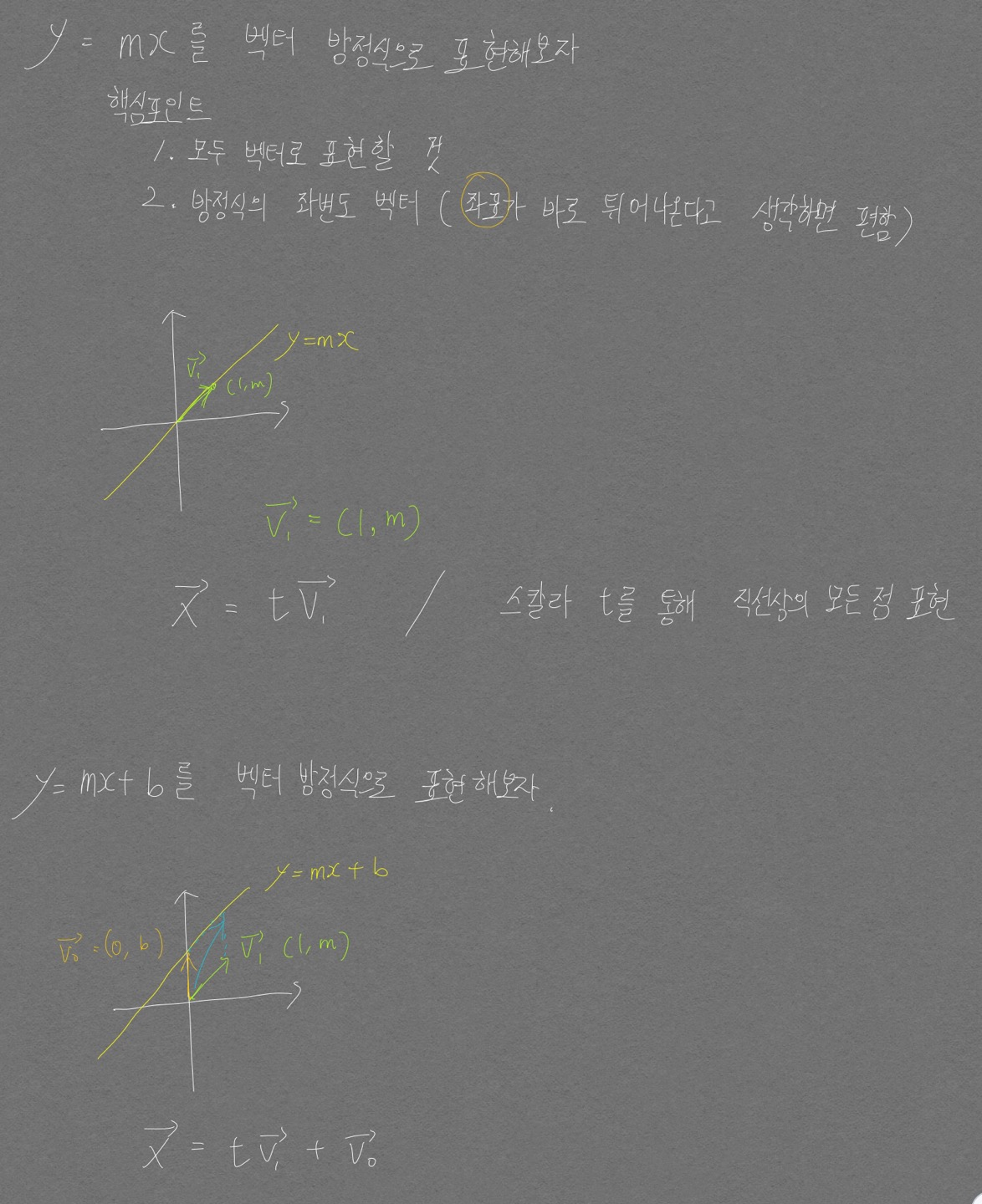
  • 평면의 벡터방정식
    • 한 점을 지나는 평면은 무수히 많음. 직선의 벡터방정식에선 한 점과 방향벡터를 통해 하나의 직선을 지정함. 평면의 벡터방정식에선 한 점과 법선벡터를 통해 하나의 평면 지정 가능

    

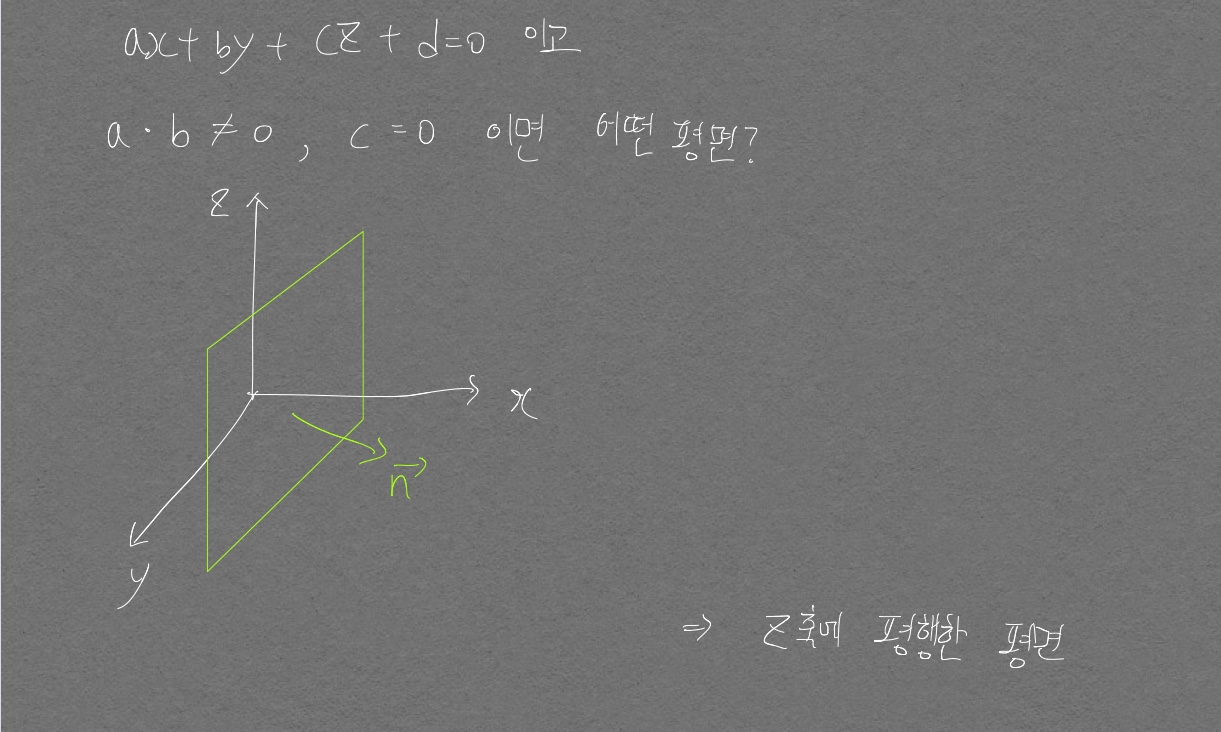
    • 벡터의 내적
      1. 외적 ⇒ 결과가 벡터
      2. 내적 ⇒ 결과가 스칼라
         • 식: $\vec{A} \cdot \vec{B} = \lvert A \rvert \times \lvert B \rvert \times \lvert cos\theta \rvert$ ⇒ 스칼라
         • 각 두 벡터의 속성값을 곱한것들을 합치면 스칼라 값이 됨
         • 항상 의문이였던 것 => 왜 저게 내적의 정의가 저렇게 되는걸까? 정의가 저러하니 쓰자는 마인드는 고등학교때 까지만이고, 깨어있는 사고를 위해 왜 저걸 내적이라고 정의하는지
           고민하고 싶음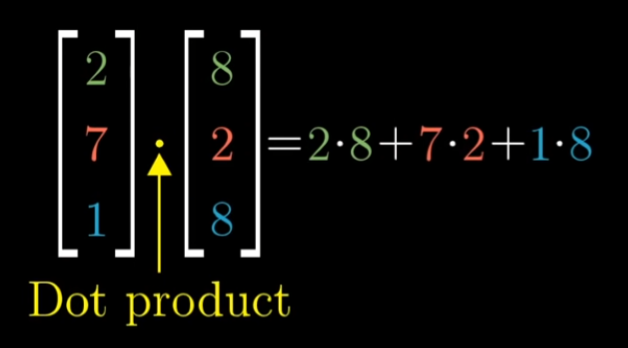
           위 투사(Projection)과 내적 공식이 무슨 관계인것인가?
         • 무슨 관계인지 파악하려면 이중성(Duality)를 알아야함
           • 이 부분은 Machine-learning 공부하면서 좀 더 작성하도록 하자
  • 문제

    1. $y = 3x + 2$의 벡터방정식

       답. $\vec{X} = (t, 3t + 2)$ 형태는 달라질 수 있음

    2. $x + 2y + 3z = 4$의 벡터방정식

       sol. 임의의 점 하나를 구해서 $\vec{V_0}$구함 $\vec{V_0}$를 기준으로 임의의 점 두개를 더 구해서 방향벡터 2개 $\vec{V_1}, \vec{V_2}$를 구함.
       혹은 법선벡터를 이용해서 더 쉽게 구할수도 있음. 여기서는 두개의 방향벡터를 이용한 풀이

       답. $\vec{X} = \vec{V_0} + t_0\vec{V_1} + t_1{V_2}$에서 임의의 점을 통해 구한 $\vec{V_0}, \vec{V_1}, \vec{V_2}$를 대입하면 됨.
       각 벡터들은 구한 임의의 점에 따라 달라질 수 있음